6장. 분기 한정법(Branch-and-Bound)
◆ 분기 한정법 (Branch and Bound)
- Branch: 가지를 나눈다
- Bound: 한계를 정한다
내가 어느쪽으로 가는 게 더 이득인지 가지를 치는 과정에서 한계를 가지고 판단하겠다 라는 뜻
되추적의 개념 + 최적화 문제에 대한 가장 좋은 해를 찾는 개념이 포함되어있다.
기본적으로 해를 찾아가는 방법은 백 트래킹.
어떤 해를 선택하느냐는 bound를 사용하며 뭐가 더 이득인지 판단.
되추적에서는 상태 공간 트리를 움직이면서 해를 찾았음. (promising 함수 사용)
분기한정법에서도 상태 공간 트리를 순회하긴 하는데, Bound 함수를 통해서 지금까지 찾은 해보다 최대한 더 좋은 해를 찾는 방향으로 나아가며, 최종적으로 가장 좋은 해를 찾아나가는 방법.
◆ 최소화 문제
최소 거리의 트래킹 코스를 찾는 문제라 하자.

팻말은 해당 코스의 최소 트래킹 코스 거리를 알려준다. 즉 항상 실제 거리 >= 팻말 표시 거리 라고 하자.
A와 B 중에서 탐사를 해야한다면, 최소 거리가 짧은 A부터 탐사할 것이다.
만약, A 탐사후 나온 결과가 B의 최소 거리인 200보다 작다면 B는 탐사할 필요가 없다.
또 만약 실제 거리가 80인 C 코스를 알고있다면, A와 B 코스를 탐사할 필요는 없다.
여기서의 팻말이 Bound 역할임. 이 코스를 탐사했을 때 얻을 수 있는 최소 거리.
◆ 최대화 문제
최대 가치를 가진 코스를 찾는다고 하자.

팻말은 해당 코스에서 얻을 수 있는 보물의 최대 가치를 알려준다. 즉 항상 실제 가치 <= 팻말 표시 가치 라고 하자.
A와 B 중에서 탐사를 해야 한다면, 최대 가치가 높은 B부터 탐사할 것이다.
만약, B를 탐사하여 나온 결과가 A의 최대 가치인 100보다 높다면 A는 탐사할 필요가 없다.
또 만약 실제 가치가 150인 C를 알고 있다면, A와 B 코스를 탐사할 필요는 없다.
여기서 팻말이 Bound 역할임. 이 코스를 탐사했을 때 얻을 수 있는 최대 이익.
◆ 분기 한정법 특징
- 상태공간 트리를 만들어 문제를 해결함
- 최적화 문제(최적의 해를 구하는 문제)에 적용할 수 있음
- 최적해를 구하려면 모든 해를 다 고려해봐야 하기 때문에, 마디를 순회하는 방법에 구애 받진 않음 (성능은 차이가 있을지라도, BFS, DFS, Best-FS 등 다 쓸 수 있음)
◆ 분기 한정법 원리
- 각 마디를 검색할 때마다 그 마디가 유망한지의 여부를 결정하기 위해, bound(한계)값을 계산한다. 이는 그 마디로부터 가지를 뻗어나가서 얻을 수 있는 해답 값의 한계를 의미함.
- 그 한계 값이 지금까지 찾은 최적의 해보다 좋지 않은 경우, 더이상 검색할 필요 없으므로 그 마디는 유망하지 않다고 할 수 있음.
◆ 0-1 Knapsack Problem
동적 계획법때 다뤘었던 배낭 문제.

가방에 들어있는 물건들의 가치인 pi 합이 최대. 무게인 wi 합은 W를 넘지 않도록.
담는 물건을 xi라 할 때 0이면 안 담고 1이면 담는 걸로 함.
◆ 0-1 Knapsack Problem - bound 개념이 없을 때의 되추적
깊이 i에서,
- 왼쪽 : item_i를 넣는 경우
- 오른쪽 : item_i를 넣지 않는 경우
로 설정함.
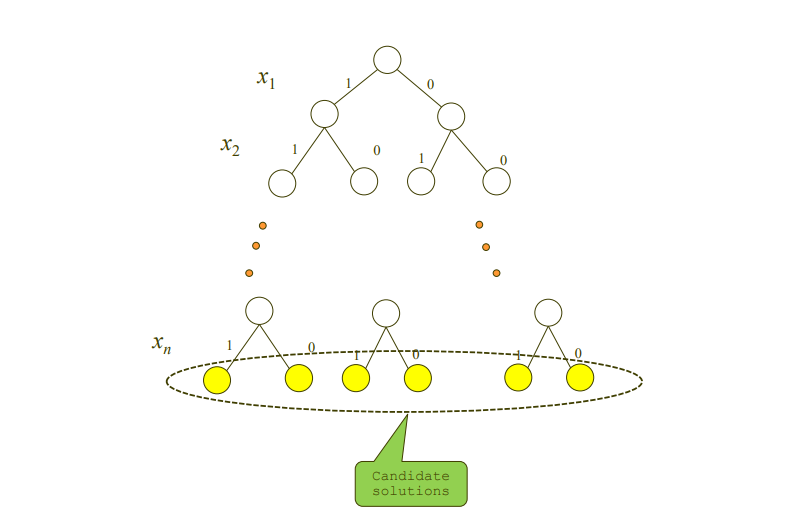
이런식으로 쭉 상태 공간 트리를 만들어나가면 답을 찾아나갈 수 있긴 함.
그러나 젤 좋은 걸 찾기 위해 모든 노드들을 다 생성해봐야 하기 때문에 좋은 방법은 아님
◆ Branch and Bound 일반적인 알고리즘
[pseudo code]
void checknode(node v) {
node u;
if(value(v) is better than best) // 이번 v로 갈 때의 가치가 지금껏 가치보다 더 좋으면
best = value(v); // 지금까지 최대 가치를 v로 설정
if(promising(v)) // 이번 v로 가는 방법이 유망하면
for(each child u of v) // v의 자식 노드들에 대해서
checknode(u); // 계속해서 유망한지, 좋은 가치인지 판단
}- best : 지금까지 찾은 제일 좋은 해답값.
- value(v) : v 마디에서의 해답값.
◆ 0-1 Knapsack Problem - bound 개념 활용시 되추적
무게당 가치가 큰 순으로 정렬하고, bound > maxprofit이면 유망.
(왼쪽- 넣음, 오른쪽- 안넣음.)
유망한지 판단하기 위해서, bound 함수를 정의해야 함.
- bound 함수 : 배낭을 빈틈없이 모두 채운다 했을 때, 현 상태에서 만들어낼 수 있는 이론적 최대 가치.(아이템을 자를 수 있다 했을때 이론적인 최대 값어치)
우선, 아이템은 무게당 가치가 감소하는 순서(큰 순서)로 정렬 가정
- profit : 그 마디에 오기까지 넣었던 아이템의 값어치의 합.
- weight : 그 마디에 오기까지 넣었던 아이템의 무게의 합.
- bound :
우선, 마디가 수준 i에 있다고 하고, 수준 k에 있는 마디에서 총무게가 W를 넘는다고 하자. 그러면 안 쪼개고 최대한 넣은 weight의 합(totweight)는 다음과 같다.
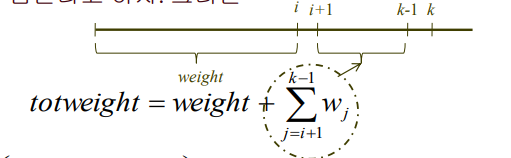
이로부터 쪼개야 하는 무게가 얼마인지 구할 수 있음. (W-totweight)
이를 활용해 이론적인 값어치 상한값을 나타내는 bound를 구하면 다음과 같다.

bound = (i까지의 이득 + 다음 거(i+1)부터 k 전까지 아이템 가치의 합) + k번째 아이템 중에서 넣을 수 있는 부분만 넣은 무게 * 무게당 가치.
bound 예시)
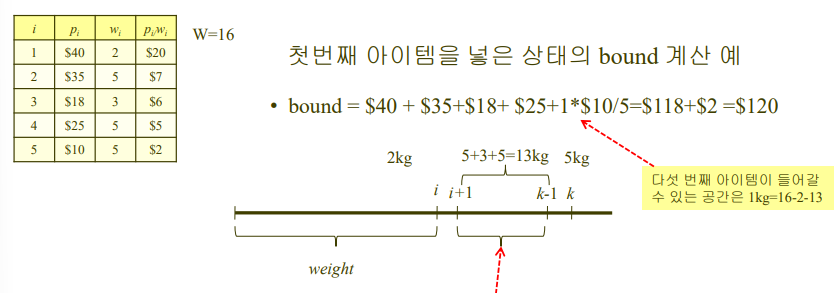
이런식~
- maxprofit : 지금까지 찾은 최선의 해답이 주는 값어치
✓ bound ≤ maxprofit 이면 수준 i에 있는 마디는 유망하지 않다. (같은 경우에도 굳이 그쪽으로 갈 필요 없음)
✓ wi와 pi를 각각 i번째 아이템의 무게와 값어치라고 하면, pi /wi 의 값(무게당 가치)이 큰 것부터 내림차순으로 아이템을 정렬한다. 이 순서로 하나씩 집어넣을지 말지 결정함. (일종의 탐욕적인 방법이 되는 셈이지만, 알고리즘 자체는 탐욕적인 알고리즘은 아니다.)
※ 초기값: maxprofit := 0; profit := 0; weight := 0
이제 실제로 해보자!
✓ 깊이우선순위(DFS)로 각 마디를 방문하여 다음을 수행한다:
1. 그 마디의 profit과 weight를 계산한다.
2. 그 마디의 bound를 계산한다.
3. weight < W and bound > maxprofit이면(유망하면), 검색을 계속한다.
그렇지 않으면, 되추적. 뒤로 돌아감.
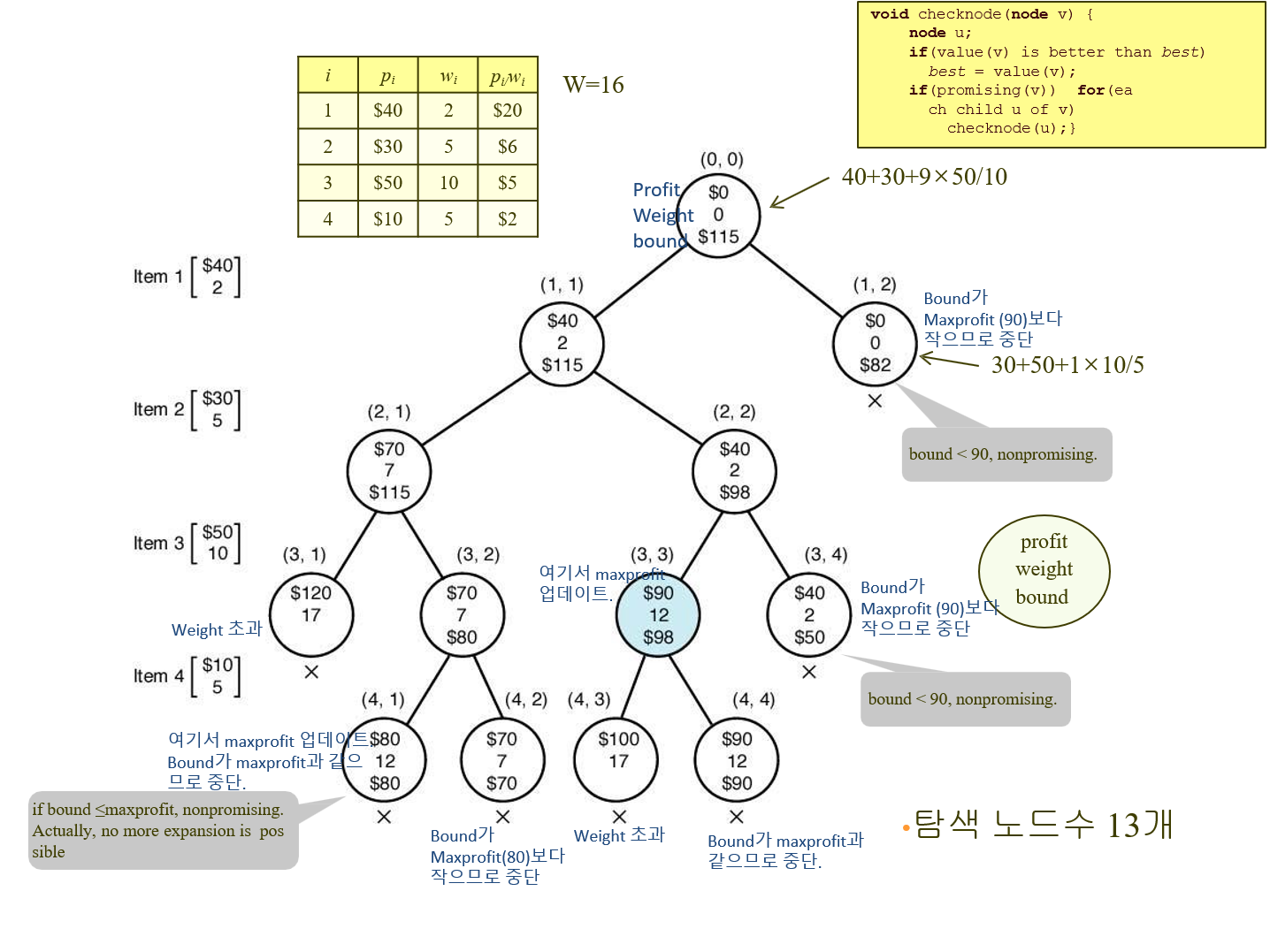
✓ 고찰: 최선이라고 여겼던 마디를 선택했다고 해서 실제로 그 마디로부터 최적해가 항상 나온다는 보장은 없다.
탐색한 노드수는 중단한 지점까지 보면 됨.
//배열 bestset
//1부터 n. bestset[i]의 값은 i번째 아이템이 최적의 해에 포함되어 있으면 Y, 아니면 N.
void knapsack(index i, int profit, int weight)
{
if(weight <= W && profit > maxprofit){ //무게 안 초과하는데 이번꺼 포함 가치가 기존보다 클때
maxprofit = profit; // 현재 아이템까지의 profit으로 maxprofit 설정
numbest = i; // 이번 인덱스를 최고아이템 인덱스로 설정
bestset = include; // 배열간 복사(지금까지 뭐가 포함되었는지)
}
if(promising(i)){ // promising에서 i번째를 넣을 공간이 있고, 이때 bound가 maxprofit보다 큰 경우 판단
include[i+1]=“yes”; // 다음거 집어넣어보자
knapsack(i+1,profit+p[i+1],weight+w[i+1]); // 넣었을때 가치와 무게 추가
include[i+1]=“no”; // 다음거 안 집어넣어보자
knapsack(i+1, profit, weight); // 현 가치와 무게 유지
}
}bool promising(index i) { //자신이 유효한지, 그리고 확장이 가능한지 확인
index j,k;
int totweight;
float bound;
if(weight >= W) // 배낭에 물건이 꽉차있다면
return false;
else{ // 그렇지 않으면
j=i+1;
bound = profit;
totweight = weight;
while ( j<=n && totweight + w[j] <= W){ // 물건을 넣을수있을 때까지 집어넣다가,
totweight = totweight + w[j];
bound = bound + p[j];
j++;
}
k=j; // 더이상 못넣는 k번째 물건을
if(k<=n)
bound = bound + (W-totweight)*p[k]/w[k]; //무게당 가치로 쪼개서 넣음
return bound > maxprofit; // 이렇게 계산한 bound가 현재 알고있는 최대가치보다 크다면 확장 유망함
}
}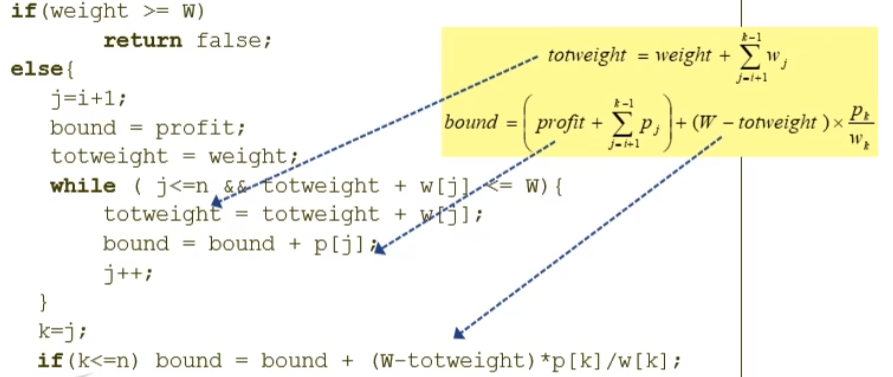
앞서봤던 공식을 그냥 구현해놓은 거임ㅇㅇ
// 실제 사용시 이런 식으로 사용
numbest=0;
maxprofit=0;
knapsack(0,0,0);
cout << maxprofit;
for (j=1; j<= numbest; j++) cout << bestset[j]; //최고아이템 인덱스까지 Y, N 출력할 것
◆ 0-1 Knapsack Problem - 시간복잡도 분석
ㆍn개의 노드를 각각 넣을지 말지 결정하기 때문에, 이 알고리즘이 점검하는 마디의 수는 2n+1-1 = Θ(2n)이다.
ㆍ만약 W=n, pi=1, wi=1, (1≤ i ≤n-1) , pn=n, wn=n 이면 최적해는 n번째 아이템을 선택하는 것이 될텐데, 그럼 앞 노드 모두 만들어놓고 결국 마지막쯤에 n을 선택하게 되어 최악이 됨.(W=n일 때, 1~n-1노드까지는 p와 w가 1이고, n노드는 p와 w가 n인 경우)
ㆍ그럼 이 알고리즘이 동적 계획법으로 설계한 알고리즘보다 좋은가?
→ 확실히 대답할 수 없다.
◆ 분기 한정(Branch and bound) 가지치기로 너비우선 검색(BFS)
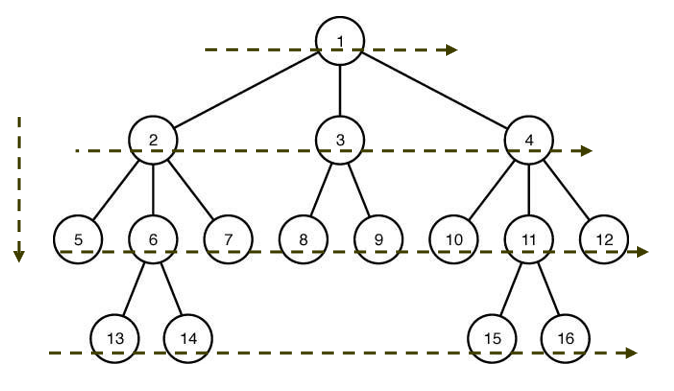
■ 일반적인 BFS 알고리즘 : queue를 사용하여 구현
처음에는 Queue에 root 노드 넣음
Queue에서 뺄 때마다 빼는 노드의 자식 노드를 넣어줌으로써 BFS 구현
[pseudo code]
void breadth_first_search(tree T) {
queue_of_node Q;
node u, v;
initialize(Q); // Q는 빈 queue로 초기화
v = root of T; // 트리의 루트를 v라고 하자
visit v; // v를 방문.
enqueue(Q,v); // Q에다 v를 넣음
while(!empty(Q)) { // Q가 비어있지 않은 동안 반복
dequeue(Q,v); // v를 빼고,
for(each child u of v) {// v의 자식노드 각각을
visit u; // 방문하고
enqueue(Q,u); // Q에다 넣음
}
}
}
■ branch and bound(분기 한정)를 적용한 BFS 알고리즘
queue를 사용하고, value와 bound 두가지 측면을 체크함.
(value는 최대 가치 업데이트를 위해 체크하고, bound는 유망한지 확인을 위해 체크)
[pseudo code]
void breadth_first_branch_and_bound(state_space_tree T, number& best) {
queue_of_node Q;
node u, v;
initialize(Q); // Q는 빈 Queue로 초기화
v = root of T; //root 노드를 v라고 하자
enqueue(Q,v); // Q에다 v 넣음
best = value(v); // v가 만들어내는 해로 best 초기화. (0-1 knapsack 의 경우 profit의 개념임.)
while(!empty(Q)) {
dequeue(Q,v); // Q에서 v 빼냄
for(each child u of v) { // v의 각 자식노드를 방문
if(value(u) is better than best) // 현재 알고있는 최고가치보다 u의 가치가 더 좋으면
best = value(u); // best 업데이트
if(bound(u) is better than best) // u넣었을 때의 이론적 최대 가치가 현재 알고있는 최고가치보다 좋으면
enqueue(Q,u); // 큐에다 u 넣기
}
}
}
■ 분기 한정 BFS를 사용해 0-1 knapsack 문제 풀기
Queue 사용해서 BFS 구현.
profit 체크 - 최대 가치 업데이트를 위해 체크
bound 체크 - 여전히 유망한지 체크
(자식의 weight, profit, level값은 내 weight, profit, level값을 포함하면서 업데이트)
[pseudo code]
void knapsack2(int n, const int p[], const int w[], int W, int& maxprofit){
queue_of_node Q;
node u,v;
initialize(Q); // Q는 빈 queue로 초기화
v.level=0; v.profit=0; v.weight=0; // 레벨(깊이), profit, weight 초기화 (루트의 값으로)
maxprofit=0;
enqueue(Q,v); // Q에다 v 넣기
while(!empty(Q)){ // Q에 원소가 남아있을 때까지
dequeue(Q,v); // Q에서 v빼기
u.level = v.level + 1; // 자식 노드 level 업데이트
//자식 노드 u를 포함하는 경우(왼쪽으로 내려가는 부분)
u.weight = v.weight + w[u.level]; // u 에서의 weight 업데이트
u.profit = v.profit + p[u.level]; // u 에서의 profit 업데이트
if(u.weight <= W && u.profit > maxprofit) // u 무게가 한도무게 이하이고, u에서의 profit이 maxprofit보다 크면
maxprofit = u.profit; // maxprofit 업데이트
if(bound(u) > maxprofit) // u를 포함했을 때, u에서의 bound가 maxprofit보다 크면
enqueue(Q,u); // 유망하므로 인큐
//자식 노드 u를 포함하지 않는 경우(오른쪽으로 내려가는 부분)
u.weight = v.weight; // weight 그대로
u.profit = v.profit; // profit 그대로
if(bound(u) > maxprofit) // u를 포함 안했을 때, u에서의 bound가 maxprofit보다 크면
enqueue(Q,u); // 유망하므로 인큐
}
}
현 단계에서 앞으로 얻을 수 있는 이익의 최대치(bound) 계산.
float bound (node u) {
index j,k; int totweight; float result;
if(u.weight >= W)
return 0;
else{
result = u.profit; // 지금까지의 이익
j = u.level+1; // 다음 레벨
totweight = u.weight; // 지금까지의 무게
while ( j<=n && totweight + w[j] <= W){ // 이 다음거부터 넣을수 있을 때까지 넣음
totweight = totweight + w[j];
result = result + p[j];
j++;
}
k=j; // 더이상 못 넣는 item을 k로 설정
if(k<=n) // k번째 item은 쪼개서 넣음
result = result + (W-totweight)*p[k]/w[k]; // 남은 무게 여분 * 무게당 가치를 곱해서 넣음
return result; //이론적 최대 이익 반환
}
}
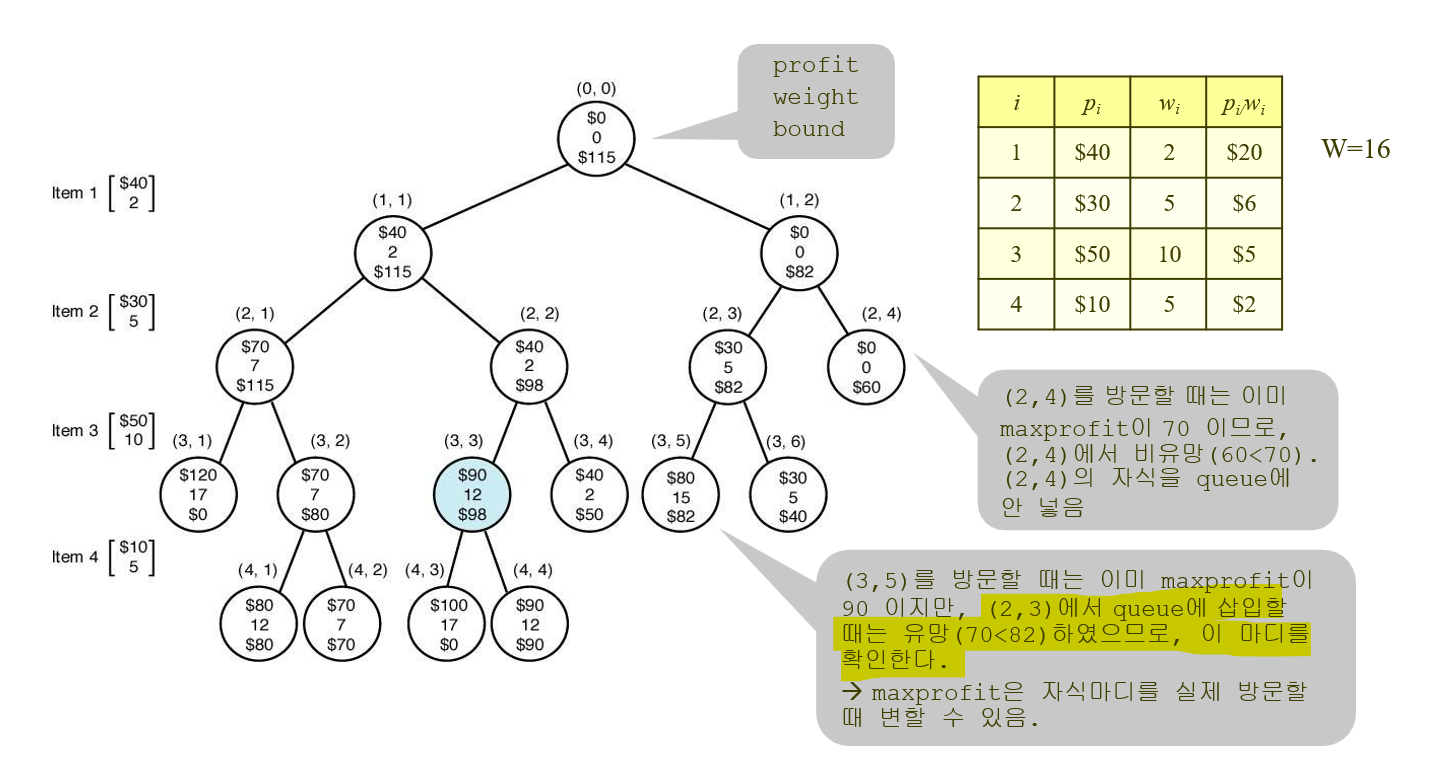
DFS로 했을 때는 검색하는 노드 개수가 13개였는데.. BFS로 하니 17개가 됨. 좋지않다!
◆ 분기한정 가지치기로 최고우선 검색 (Best First Search)
bound가 높은 순으로 정렬된 PQ사용.
최적의 해답에 더 빨리 도달하기 위한 전략!
- 주어진 마디의 모든 자식마디를 검색한 후,
- 유망하면서 확장되지 않은(unexpanded) 마디를 살펴보고,
- 그 중에서 가장 좋은(최고의) 한계치(bound)를 가진 마디를 확장한다
최고우선검색(Best-First Search)은 DFS나 BFS에 비해서 좋아짐!
최고의 bound를 가진 마디를 우선적으로 선택하기 위해서 우선순위 대기열(priority queue)을 사용한다.
우선순위 대기열은 힙(heap)을 사용하여 효과적으로 구현할 수 있다. (n lg n)
※ Heap에서 트리와 배열의 연관성
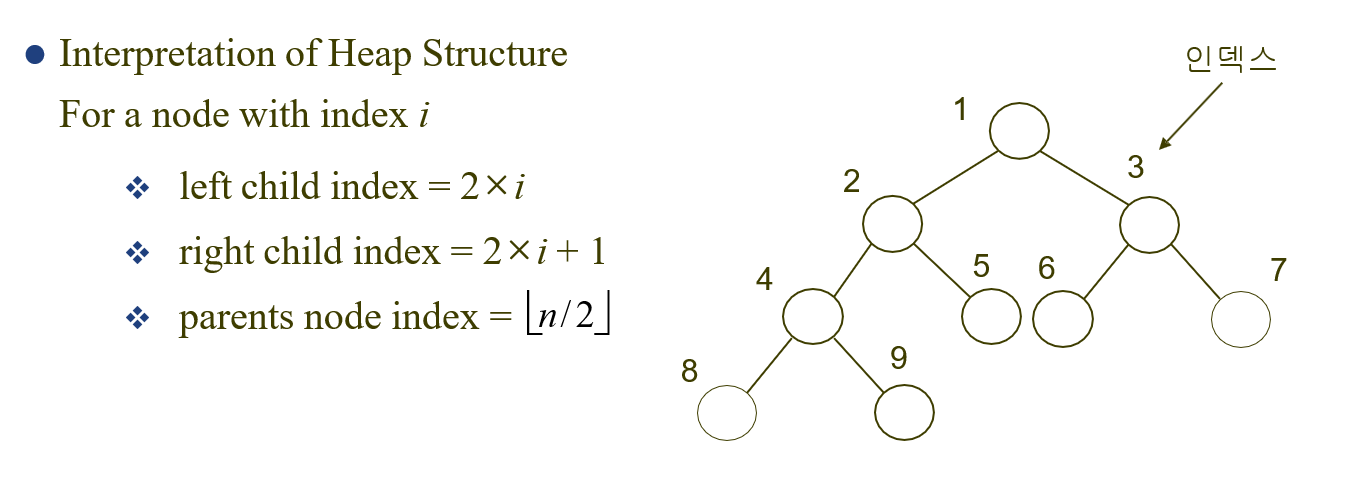
즉 굳이 트리 구조로 저장하지 않고 배열로 저장할수도 있다는 점~
■ 일반적인 최고우선 검색 알고리즘
PQ를 사용해 bound가 높은 것부터 갖고옴
value와 bound 각각 체크(업데이트 확인용, 유망한지 확인용)
[pseudo code]
void best_first_branch_and_bound(state_space_tree T, number& best) {
priority_queue_of_node PQ;
node u,v;
initialize(PQ); // PQ를 빈 큐로 초기화
v = root of T; // v에 루트값 넣음
best = value(v); // 초기 best는 v일때 가치로 초기화
insert(PQ,v); // PQ에다 v넣음
while(!empty(PQ)) { // PQ가 비어있지 않을 때까지
remove(PQ,v); // bound가 가장 높은 노드 제거(항상 루트를 제거)
if(bound(v) is better than best) // 마디가 아직 유망한 지 점검(bound가 best보다 큰지)
for(each child u of v) { // v의 각 자식 노드 u에 대해
if(value(u) is better than best) // u를 넣었을때의 가치가 best보다 크면
best = value(u); // best 업데이트
if(bound(u) is better than best) // u가 아직 유망하다면
insert(PQ,u); // PQ에 넣음
}
}
}
■ 최고우선 검색을 활용한 knapsack
PQ를 활용해 bound가 높은 것부터 갖고옴.
포함할거면 value값 업데이트 확인.
유망하면 enque
[pseudo code]
void knapsack3(int n, const int p[], const int w[], int W, int& maxprofit){
priority_queue_of_node PQ;
node u,v;
initialize(PQ); //PQ 초기화
v.level = 0; v.profit = 0; v.weight = 0; // v 멤버들을 root를 나타내도록 초기화
maxprofit = 0;
v.bound = bound(v); //v의 bound(한계값) 계산
insert(PQ,v); //PQ에 v 넣기
while(!empty(PQ)){ // PQ가 비어있지 않을 때까지
remove(PQ,v); // bound값이 가장 큰 노드(root 노드) 추출
if(v.bound > maxprofit){ // v가 아직 유망하다면
u.level = v.level + 1; // 자식노드 u 세팅
// u를 포함하는 경우
u.weight = v.weight + w[u.level]; //u에서의 weight 업데이트
u.profit = v.profit + p[u.level]; //u에서의 profit 업데이트
if(u.weight <= W && u.profit > maxprofit) //u에서의 profit이 maxprofit보다 크면
maxprofit = u.profit; // maxprofit 업데이트
u.bound = bound(u); // u를 포함했을 때, u에서의 bound 계산
if(u.bound > maxprofit) // u가 아직 유망하다면
insert(PQ,u); // PQ에 넣기
// u를 포함하지 않는 경우
u.weight = v.weight; // u에서의 weight 그대로
u.profit = v.profit; // u에서의 profit 그대로
u.bound = bound(u); // u를 포함하지 않았을 때, u에서의 bound 계산
if(u.bound > maxprofit) // u가 아직 유망하다면
insert(PQ,u); // PQ에 넣기
} // if
} // while
}
//bound 함수는 이전과 같다.
float bound (node u) {
index j,k; int totweight; float result;
if(u.weight >= W)
return 0;
else{
result = u.profit; // 지금까지의 이익
j = u.level+1; // 다음 레벨
totweight = u.weight; // 지금까지의 무게
while ( j<=n && totweight + w[j] <= W){ // 이 다음거부터 넣을수 있을 때까지 넣음
totweight = totweight + w[j];
result = result + p[j];
j++;
}
k=j; // 더이상 못 넣는 item을 k로 설정
if(k<=n) // k번째 item은 쪼개서 넣음
result = result + (W-totweight)*p[k]/w[k]; // 남은 무게 여분 * 무게당 가치를 곱해서 넣음
return result;
}
}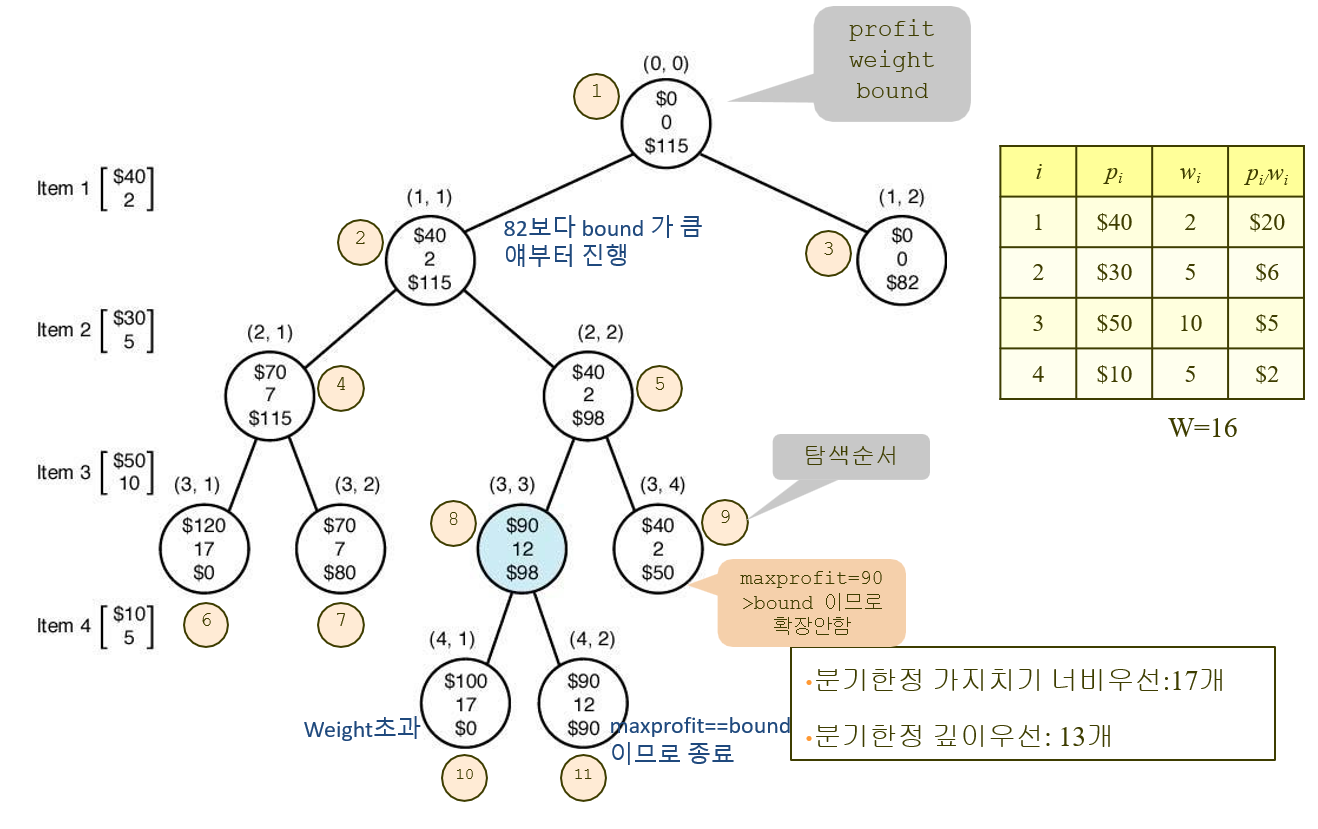
1 - 2,3 확장
2 – 4,5 확장
4 – 6,7 확장. 6은 enque 안함 (weight 초과)
5 – 8,9 확장. 9는 enque 안함(maxprofit > bound) <- 주의. 5번 다음 레벨을 넣는 경우인 8번부터 먼저 보기 때문에, 9번 볼 때는 이미 maxprofit이 업데이트된 후임. 그래서 애초부터 PQ에 넣지를 않음
8– 10,11 확장. 10은 enque 안함(weight 초과)
11 – 확장 안함 (maxprofit == bound)
3 – 확장 안함 (maxprofit > bound)
7 – 확장 안함 (maxprofit > bound)
◆ 외판원 문제
하나의 노드에서 출발하여 다른 노드들을 각각 한번씩만 방문하고, 다시 출발노드로 돌아오는 가장 짧은 일주여행경로(tour)를 결정하는 문제
이 문제는 음이 아닌 가중치가 있는, 방향성 그래프로 나타낼 수 있다.
그래프 상에서 일주여행경로(tour) 또는 해밀토니안 회로(HC; Hamiltonian Circuit)는 한 정점을 출발하여 다른 모든 정점을 한번씩만 거쳐서 다시 그 정점으로 돌아오는 경로를 의미함.
여러 개의 일주여행경로 중에서 길이가 최소가 되는 경로가 최적일주여행 경로(optimal tour)가 된다.
◆ 외판원 문제 - 무작정 알고리즘
가능한 모든 일주여행경로를 다 고려한 후, 그 중에서 가장 짧은 일주여행경로를 선택한다.
가능한 일주여행경로의 총 개수는 (n - 1)!
◆ 외판원 문제 - 분기한정법
상태공간트리 구축 방법.
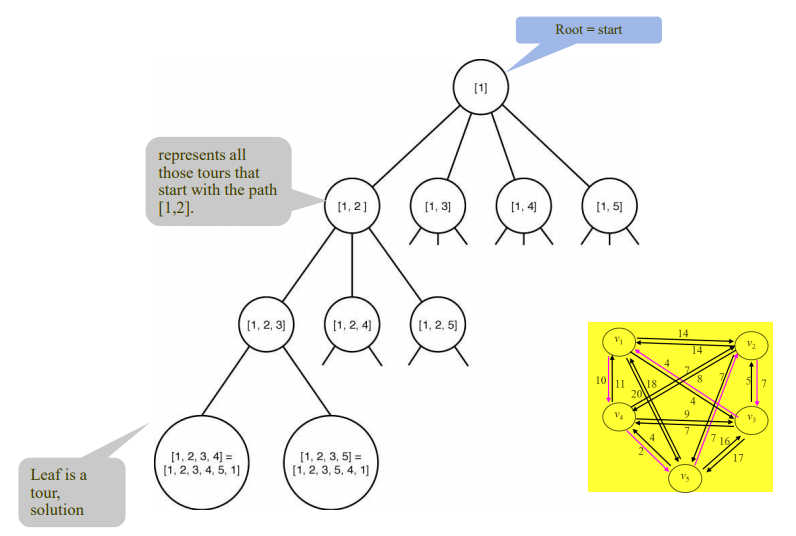
각 노드는 출발 노드로부터의 일주여행경로를 나타냄.
루트 노드의 여행경로는 [1]이고, 1레벨에서는 [1,2], [1,3], .. 이런식으로 진행.
쭉 뻗어나가다가 n-1레벨에 도달하면 더이상 확장 안해도 됨. 마지막남은 n번째 값이랑, (다시 돌아온) 출발 값 넣어주면 되기 때문.
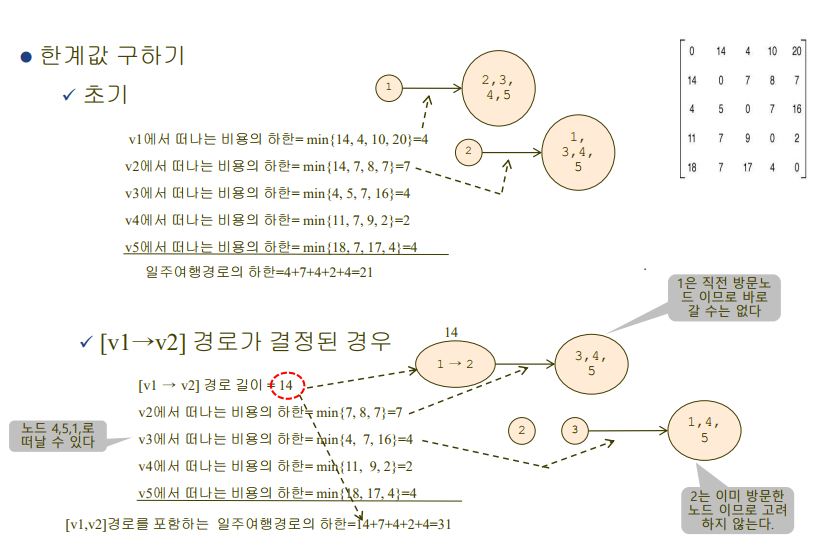
각 노드에서 갈 수 있는 노드로의 비용 집합 중 최솟값을 하나씩 고름.
이런식으로 일주 여행경로의 하한값(이론상 최솟값)을 업데이트해나가면서 최단 경로와 비용을 구함.
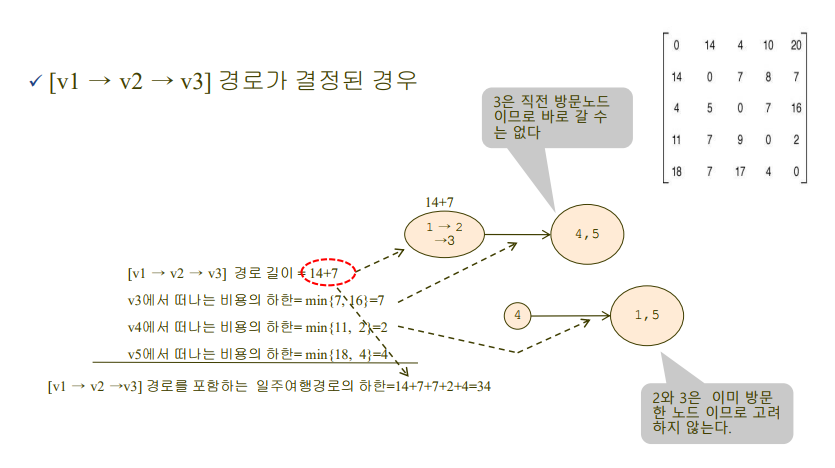
분기한정 가지치기로 최고우선 검색(Best First Search)를 하여 상태 공간 트리를 만들어나간다.
Bound가 작은 것부터 정렬하도록 PQ(Min Heap)에 넣자.
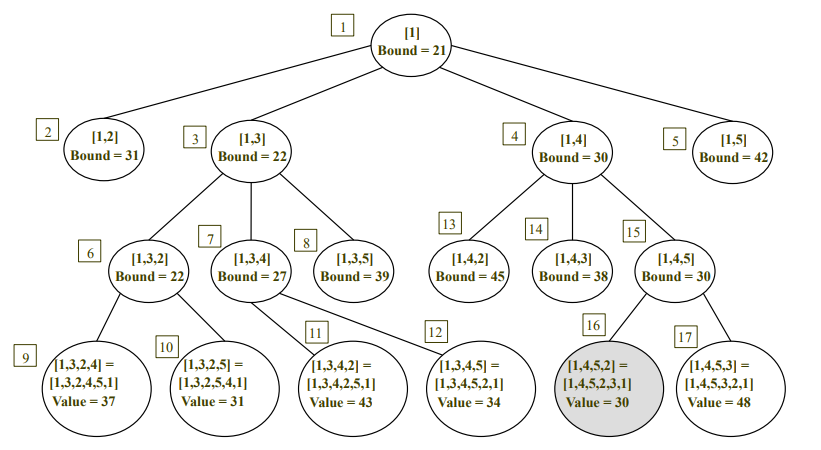
[순서]
1 - 2,3,4,5로 확장
3 - 6,7,8로 확장
6 - 9,10으로 확장(leaf). min = 31
7 - 11,12로 확장(leaf)
4 - 13,14,15로 확장(13,14는 Bound > min 이므로 enque안함)
15 - 16,17로 확장(leaf). min = 30
2 - Bound > min 이므로 확장 안함
8 - Bound > min 이므로 확장 안함
5 - Bound > min 이므로 확장 안함
void travel2(int n, const number W[][],ordered-set& opttour, number& minlength)
{
priority_queue_of_node PQ;
node u,v;
initialize(PQ);
v.level = 0; v.path=[1];
v.bound = bound(v);
minlength= ∞;
insert(PQ,v);
while(!empty(PQ)){
remove(PQ,v);
if(v.bound < minlength){
u.level=v.level + 1;
for(all i such that 2≤i≤n && i is not in v.path){
u.path = v.path;
put i at the end of u.path;
if(u.level == n-2){
put index of only vertex not in u.path at the end of u.path;
put 1 at the end of u.path;
if (length(u) < minlength){
minlength = length(u);
opttour = u.path;
}
}
else{
u.bound = bound(u);
if(u.bound < minlength)
insert(PQ,u);
} /* else*/
} /* for */
} /* if */
} /* while */
}
float bound(node u)
{
homework
}
※ 분기한정 가지치기로 최고우선검색 알고리즘의 시간복잡도는 지수적이거나 그보다 못하다!
- 다시 말해서 n = 40이 되면 문제를 풀 수 없는 것과 다름없다고 할 수 있다.
- 다른 방법이 있을까?
- 근사(approximation) 알고리즘:
- 최적의 해답을 준다는 보장은 없지만, 무리 없이 최적에 가까운 해답을 주는 알고리즘.
- 최적의 해답을 준다는 보장은 없지만, 무리 없이 최적에 가까운 해답을 주는 알고리즘.