센로그
2. Vectors and Matrices 본문
◆ Vectors and Matrices
3D 그래픽에서는 많은 벡터와 행렬 연산이 나오기 때문에 잘 알고있어야 함~
◆ 벡터의 크기 (Magnitude)
||v|| = \(\sqrt{a² + b²}\)
Vector v = (3,1)일 때 v의 크기 ||v|| = \(\sqrt{3² + 1²}\) = \(\sqrt{10}\)
◆ 벡터의 연산 - 덧셈, 뺄셈, 상수배
덧셈, 뺄셈, 상수배는 각각 요소별로 계산하면 됨
< 예시 >
Vector a = (1,2) 이고 Vector b = (2,1)일 때
- a + b = (3,3)
- a - b = (-1,1)
- 3a = (3,6)
◆ 벡터의 연산 - 스칼라곱 (Dot Product, Scalar Product)
aㆍb = a₁b₁ + a₂b₂ = ||a||||b||cosθ
내적은 정사영의 크기.
< 예시 >
Vector a = (1,2) 이고 Vector b = (3,4)일 때
a와 b의 내적 aㆍb = 1*3 + 2*4 =11

기하학적으로, aㆍb 는 ||a||||b||cosθ 이다.
< 특징 >
- aㆍa = 1
- a, b가 서로 수직인 경우, aㆍb = 0
- aㆍb = bㆍa
내적은 Lighting을 계산할 때 사용됨!
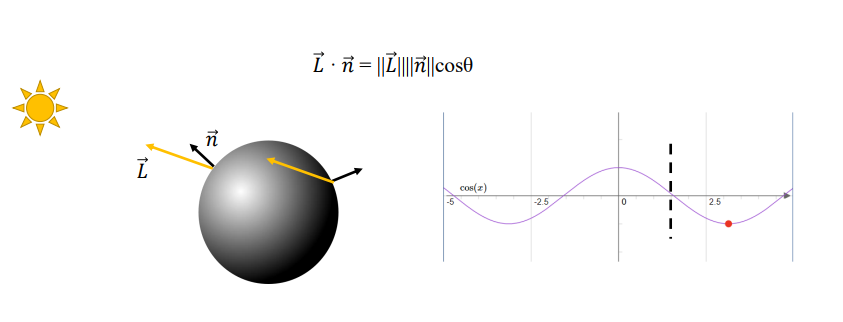
* 스칼라 곱(dotproduct)과 내적(inner product)의 차이!스칼라 곱은 실수 벡터 공간에서 정의되고, 내적은 복소수 벡터 공간에서 정의된다. |
◆ 벡터의 연산 - 벡터 곱 (Cross Product, Vector Product)
u x v는 (u ∧ v 라고도 쓴다!) 행렬식(Determinant)으로 계산한다.
오른손 법칙!

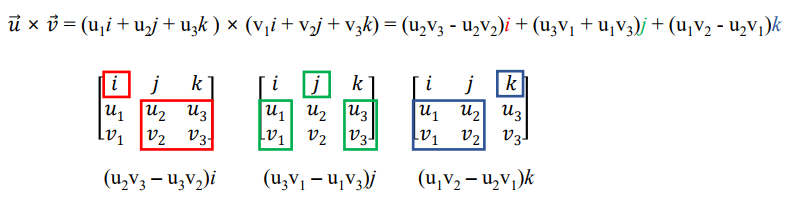
기하학적으로, || a x b ||는 ||a||||b||sinθ 이다. 아래 평행사변형의 면적을 의미함.

< 특징 >
- a x a = 0
평행한 벡터끼리는 평행사변형을 만들 수 없다.
* 벡터 곱(cross product)과 외적(outer product)의 차이!벡터 곱은 벡터로 보고 곱한 것이고, 외적은 행렬로 보고 곱한 것임.따라서 벡터 곱의 결과는 벡터인 반면, 외적의 결과는 행렬이다. [ 벡터곱 ]   [ 외적 ]  |
◆ 단위 벡터 (Unit Vector)
크기(magnitude)가 1인 벡터

: vector a의 단위벡터
다음과 같이 표기하면 단위벡터임
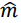
: m햇 이라고 읽음
보통 알파벳 위에 ^ 표시를 쓰고, '햇' 이라고 읽는다.
◆ 항등 행렬 (Identity Matrix)
주대각선의 원소가 모두 1이며 나머지 원소는 모두 0인 정사각 행렬

- AI = IA = A
어떤 행렬 A에 항등 행렬을 곱한 결괏값은 자기자신이다.
◆ 행렬의 성질
A, B, C가 행렬이라 하자.
- A + B = B + A
- (A + B) + C = A + (B + C)
- A(B + C) = AB + BC
- AB != BA
- (AB)C = A(BC)
◆ 전치 행렬 (Transpose Matrix)

◆ 역행렬 (Inverse Matrix)
행렬 A의 역행렬은 다음과 같이 계산할 수 있다.

당연하게도, det(A) == 0이면 역행렬이 존재하지 않는다.
'게임 > 그래픽 프로그래밍' 카테고리의 다른 글
| 5. Input Assembler & Vertex Processing(2) (0) | 2023.05.12 |
|---|---|
| 4. Input Assembler & Vertex Processing(1) (4) | 2023.05.12 |
| 3. Spaces and Transforms (0) | 2023.04.25 |
| 1. Modeling (2) | 2023.03.14 |
| Graphics Rendering Pipeline 그래픽스 렌더링 파이프라인 (3) | 2023.02.04 |
Comments




