센로그
8장. 계산 복잡도: 검색 문제 본문
정렬 문제의 계산 복잡도는 O(n lg n)이라는 걸 7장에서 증명했었다.
이번에는 검색 문제에 대해서 알아보자!
◆ 키를 비교함으로만 검색을 수행하는 경우의 하한
검색 문제란,
n개의 키를 가진 배열 S와 어떤 키 x가 주어졌을 때, x = S[i]가 되는 인덱스 i를 찾는 것.
만약 x가 배열 S에 없을 때는 오류(F)로 처리한다.
이분 검색의 경우, 시간복잡도가 W(n) = floor(lg n) + 1이 되는데, (floor은 바닥 함수를 의미함)
정렬되어있을 때 키를 비교함으로만 검색을 수행하는 경우 이분 검색보다 더 좋은 알고리즘은 없다!
이진 검색과 순차 검색의 결정 트리를 비교하면서 이를 살펴보자.
■ 이진 검색의 결정 트리.

■ 순차검색의 결정 트리

순차검색은 루트부터 시작해서 한쪽으로만 쭉 연결될 수밖에 없을 것임!
위 그림에서, 각 경로는 최대 7개의 큰 마디를 가지게 될 것. 이진 검색에서보다 안좋음!
< 결정 트리의 특성 >
ㆍroot 노드에서부터, 배열 S의 가능한 모든 결과로 도달하기위한 경로가 있다면 결정트리를 유효하다(valid)라고 한다.
ㆍ모든 leaf node가 도달 가능한 노드로 이루어진 결정트리를 가지쳐 졌다(pruned)라고 한다.
ㆍ값을 비교할 때의 결과는 3가지(<, =, >) 이므로, 결정 트리에서 한 노드는 3개의 자식 노드를 가짐.
< 최악인 경우 하한 찾기! >
최악의 경우 비교하는 횟수는 결정트리의 root에서 leaf까지 가장 긴 경로상의 비교 노드 수, 즉 (트리의 depth + 1)이다.
다음 두가지 보조 정리를 통해 트리 depth의 하한을 통해, 최악인 경우 비교하는 횟수를 확인해보자.
보조정리 1. n이 이진 트리의 노드 개수이고, d가 깊이라면 d >= floor(lg n) 이다.

한 부모당 최대 2개의 자식을 가지기 때문에, 위와같이 식을 쓰고 정리해서 증명할 수 있다.
보조정리 2. n개의 다른 키 중에서 어떤 키 x를 찾는 가지친 유효 결정트리(pruned, valid)는 비교하는 노드가 최소한 n개 있다. 즉, 비교하는 노드가 최소한 n개는 있어야 어떤 경우에도 x를 찾을 수 있다(valid)는 뜻.
이 둘을 조합해보자! n개의 다른 키 중에서 어떤 키 x를 찾는 유효한 결정 트리의 경우, 비교하는 노드가 n개는 있어야 한다. 노드가 n개인 경우, 트리의 깊이 d >= floor(lg n)이다. 따라서, 최악의 경우 비교 횟수는 floor(lg n) + 1이 된다.
그런데 아까 이진 검색의 복잡도가 W(n) = floor(lg n) + 1 이었다!
따라서 이진 검색이 검색 문제에서 최선의 해결 알고리즘이라는 것을 알 수 있당.
비슷한 방법으로 풀면, 평균의 경우 하한은 floor(lg n) - 1 이 나온다~
[pseudo code]
void binsearch(int n, const keytype S[], keytype x, index& location) {
index low, high, mid;
low = 1; high = n;
location = 0;
while (low <= high && location == 0) {
mid = (low + high) / 2; // divided by an integer
if (x == S[mid])
location = mid;
else if (x < S[mid])
high = mid – 1;
else
low = mid + 1;
}
}
◆ 검색의 하한
그렇다면 검색의 하한을 개선할 수 있을까?
=> 비교로 검색하는 게 아니라, 다른 추가적인 정보를 이용해 검색한다면 가능하다!
추가적인 정보란 어떤 걸까?
■ 예를 들자면, 몇번째 데이터가 어느정도 범위 내에 있다는 정보를 안다고 하자.
즉, 첫 번째 x가 0~9중 하나이고, 두 번째 x는 10~19중 하나이고... 열 번째 x 90~99중 하나라는 정보를 알고있다고 하자. 검색키 x가 0보다 작거나 99보다 크면 바로 검색이 실패임을 알 수 있고, 그렇지 않으면 x와 s[1+x div 10]을 비교하면 됨!

■ 또 다른 예시로 선형 보간법(linear interpolation)이 있다.

두 점의 값이 주어졌을 때, 그 두 점의 값을 바탕으로 두 점 사이에 있는 점의 값을 (선형적으로) 추정하는 방법.
이처럼 데이터의 위치에 대한 것을 보간을 통해 추정해서 검색하는 방법을 보간 검색법이라고 함.
◆ 보간 검색법
일반적으로 데이터가 가장 큰 값과 가장 작은 값이 균등하게 분포되어 있다고 가정하여,
키가 있을만한 곳으로 바로 가서 검사해보는 방법. 즉, 키의 값 자체를 이용하는 방법

S[low]와 S[high]를 이용해 x가 있을만한 곳으로 바로 가서 검사.

위와같이 선형 보간 방식으로 mid index를 계산!
그러고나서 mid를 기준으로 이진 검색을 실시하는 것임. (mid 갱신 방법도 위와 같음 ㅇㅇ)
평균의 경우, 복잡도 A(n) = lg(lg n)
최악의 경우, 즉 데이터가 균등하게 있지 않은 경우에는 시간복잡도가 순차검색과 같다. (O(n) = n)
[1, 2, 3, 4, 5, 6, 7, 8, 9, 100] 중에서 10을 찾는 경우 mid값은 계속 low값이 될 것이기 때문
[pseudo code]
void interpsrch(int n, const number S[], number x, index& i){
index low, high, mid;
number denominator;
low =1;
high=n; //배열 index는 1~n까지(수도코드)
i=0; //정답 i를 찾기 전까지 0
if(S[low] <= x <= S[high])
while (low <= high && i==0){ //low<=high이고, 아직 답을 찾지 못했다면
// mid값 갱신
denominator = S[high] – S[low];
if(denominator == 0) // 젤 큰거에서 젤 작은거 뺀 값이 0이라면
mid = low; //둘이 같은 것이므로 그 값으로 mid를 설정
else // 아직 가운데 원소가 남아있다면
mid = low + floor(((x – S[low])*(high – low))/denominator); //low, high와 x의 비율을 통해 mid 갱신
// 비교
if (x==S[mid])
i = mid;
else if ( x < S[mid])
high = mid -1;
else
low = mid + 1;
}
}
◆ 보강된 보간 검색법(robust interpolation search)
mid값이 양쪽 사이드는 되지 않도록 하는 방식
이전에, 데이터가 너무 불균등한 경우에는 순차검색처럼 된다는 사실을 언급했다.
이를 방지하기 위해서는 mid값이 양쪽 사이드는 되지 않도록 하는 방식을 사용해야 함!
gap 변수를 사용하는 방법이다. 절차는 다음과 같다.
1. gap의 초기값 = floor(sqrt(high - low + 1))
2. mid값을 선형보간법으로 구한다.3. 다음 식으로 새로운 mid값을 구한다.
mid = MIN (high - gap, MAX(mid, low + gap))
이전 예시에 보강된 보간 검색법을 적용해보자.

보강된 보간검색의
평균의 경우는 A(n) ≒ Θ(lg(lg n)) 이고
최악의 경우는 W(n) ≒ Θ((lg n)²)이다.
최악의 경우가 기존보다 좋아졌다~
◆ 트리 구조를 사용한 동적 검색
■ 검색의 분류
- 정적검색(static searching): 데이터가 한꺼번에 저장되어 추후에 추가나 삭제가 이루어지지 않는 경우에 이루어 지는 검색, 즉 예를 들면 OS명령에 의한 검색.
=> 배열 사용 - 동적검색(dynamic searching): 데이터가 수시로 추가 및 삭제되는 유동적인 경우. ex) 비행기 예약 시스템.
=> 트리구조 사용
■ 이진 검색 트리 (Binary Search Tree)를 사용하는 이유
- inorder(왼-나-오)로 traversal을 하면 정렬된 순서로 데이터를 추출할 수 있음!
-
평균적으로 좋은 성능 보장
- 동적으로 트리에 아이템이 추가되고 삭제되므로 트리가 항상 균형(balance)을 유지한다는 보장은 없다
- 최악의 경우는 연결된 리스트(linked list)를 사용하는 것(skewed tree)과 같은 효과를 보이기도 함.
- 그럼에도 불구하고, 랜덤하게 아이템이 추가되는 경우에 대체로 트리가 균형을 유지함
=> 평균적으로 효율적인 검색시간을 기대할 수 있음! - 데이터 추가 및 삭제시 효율적임. 사용하기 편함


◆ 이진 검색 트리의 분석
이진 검색트리에서 검색하는 아이템 x가 n개의 아이템 중 하나가 될 확률이 동일하다고 가정하면,
이진 검색트리의 평균 검색시간은 대략 A(n) = 1.38 lg n이 된다.
== 생성 가능한 모든 이진 검색트리에 대한 평균 검색시간.
[증명]

- root에 k번째로 작은 아이템이 있다고 가정하자. 이 경우의 평균 검색 시간을 A(n|k)라고 하자.
- root 기준, left subtree에는 k-1개의 노드가 있고, right subtree에는 n-k개의 노드가 있다.
- left subtree를 검색하는 평균 검색 시간을 A(k-1), right subtree를 검색하는 평균 검색 시간을 A(n-k)라 하자.
- x가 left subtree에 있을 확률은 (k-1)/n이고, right subtree에 있을 확률은 (n-l)/n이 된다.

계산결과 C(n) ≒ 1.38(n+1)lg n이 된다. 결론적으로 A(n)≒ 1.38lg n 이 된다.
◆ 검색시간 향상을 위한 트리구조
항상 균형을 만들어서 검색 시간을 짧게 유지하도록 하는 이진트리구조.
< 종류 >
- AVL 트리 : 아이템 추가/삭제/검색이 모두 Θ(lg n)
- B-트리 : leaf 노드들의 depth를 항상 같게 유지. 아이템 추가/삭제/검색이 모두 Θ(lg n),
- red-black 트리: 아이템 추가/삭제/검색이 모두 Θ(lg n)
균형 트리를 맞춰주게 되면 검색에선 효과적이지만, 추가적인 작업을 해야한다는 단점은 있다.
◆ AVL 트리
좌, 우 subtree의 높이 차가 최대 1인 이진 검색트리

■ AVL 트리에서, 데이터 추가시 균형을 유지하는 방법!
총 4가지 경우에 대한 조작 방법이 있다.
case 1. RR rotation

a가 추가되면, c 입장에서 left subtree 깊이는 2, right subtree 깊이는 0으로 AVL이 아니다.
이경우, 그림처럼 오른쪽으로 돌려서 b를 위로 올려주고 a와 c를 자식 노드로 만들어줌.
case 2. LR rotation

d가 추가되면, e의 입장에서 left subtree 깊이는 3, right subtree 깊이는 1이므로 AVL이 아니다.
이경우, 그림처럼 왼쪽으로 돌리고 오른쪽으로 돌려서 AVL로 재구성해줌.
(d,e,f의 관계는 d<e<f인게 확실하므로 저런식으로 구성)
case 3, case 4는 각각 case 1, case 2의 반대 경우를 의미한다.
◆ B-tree - 2-3 tree
2-3 tree는 B-tree 중 가장 간단한 형태임.
< 특징 >
✓ 각 노드에는 키가 하나 또는 둘 존재

그림처럼, [B보다 작은/B보다 큰 데이터] 또는 [B보다 작은/B와 C 사이/C보다 큰 데이터] 를 가리키는 포인터가 존재한다.
✓ 각 내부노드의 자식 수는 키의 수+1
✓ 어떤 주어진 노드의 왼쪽(오른쪽) sub트리의 모든 키들은 그 노드에 저장되어 있는 노드보다 작거나(크거나) 같다.
✓ 모든 leaf 노드는 수준이 같다
✓ 데이터는 트리 내의 모든 노드에 저장
■ 2-3 트리에서, 데이터 추가 시 균형을 유지하는 방법!

(a) 각 노드는 키가 하나 또는 두 개 있고, 모든 leaf 노드는 depth가 같은 2-3 tree임을 확인할 수 있다.
(b) 35가 추가된 상황을 가정해보자. 35가 추가되면, leaf 노드에 키가 3개가 되어서 2-3 트리가 아니게 됨. 따라서, 세 데이터 중 가운데 데이터(30)를 부모 노드로 올린다.

(c) 30이 부모로 올라갔는데, 또 키가 3개가 됐다! 다시 셋중 가운데 데이터(20)를 부모로 올린다. 그리고 셋중 왼쪽, 오른쪽에 있던 데이터를 분리해서 자식 노드와 연결한다.
(d) 20이 부모로 올라가니, 이번에는 루트가 키가 3개가 됐다! 그러면 이번에도 셋중 가운데 데이터(15)를 위로 올리고 자식 노드를 분할한다.
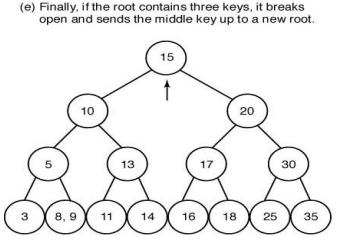
(e) 2-3 트리 완성~
◆ 해슁 (Hashing)
만약 키가 주민등록번호인 경우, 해당 번호의 저장소를 모두 만들 수는 없을거다. 10¹³개를 어떻게 다 저장해!
그럼 어떻게 할까?
=> Hashing을 이용해보자!
■ Hash
크기가 100인 배열(0~99의 index를 가진)을 만든 후에, 키를 0~99 사이의 값을 가지도록 해쉬(hash)한다.
여기서 해쉬함수는 키를 배열 index 값으로 변환하는 함수이다. (해쉬함수의 예: h(key) = key % 100)

h(key) = key % 100라 하자.
이 경우, 100키가 모두 서로 다른 해쉬값을 가질 확률은 얼마나 될까? (100개의 데이터가 각각 다른 방에 저장될 확률)

그럴 확률은 거의 없다고 보면 된다. 즉, 2개 이상의 키가 같은 해쉬값을 가질 확률이 크다! 라는 것.
즉, 충돌(collision)이 발생할 확률이 크다는 것이다.
=> 충돌을 피하거나, 충돌이 발생했을 때도 계속해서 데이터를 저장할 수 있는 방법이 필요하다!
◆ Hash - Solution to avoid collision
충돌을 피하기 위한 방법으로는 크게 두가지 방법이 있음.
- open hashing (linked list 사용)
- closed hashing (array 사용)
◆ open hashing
ㆍhash 값을 헤드로 갖고, 헤드 값에 해당되는 데이터들을 linked list 형식으로 연결하는 형태. 바구닁

ㆍopen hashing의 경우 모든 키가 같은 해쉬값을 가질 확률은 거의 없음. 어느정도 나뉘서 분포된다는 것~
ㆍ해슁이 효율적으로 작동하기 위해서는 키가 바구니에 균일하게 분포해야 함!
=> n개의 키와 m개의 바구니가 있을 때 각 바구니에 평균적으로 n/m개의 키를 갖게 하면 됨!
ㆍn개의 키가 m개의 바구니에 균일하게 분포되어 있다면, 검색에 실패한 경우 비교 횟수는 n/m이 됨. (==바구니 안쪽으로 들어가서 n/m 크기의 데이터를 끝까지 순차검색한 횟수)
ㆍn개의 키가 m개의 바구니에 균일하게 분포되어 있고, 각 키가 검색하게 될 확률이 모두 같다면, 검색에 성공한 경우 비교 횟수는 n/2m + 1/2이 됨. (바구니 안쪽으로 들어가서 n/m 크기의 데이터를 순차검색한 평균 시간)
◆ closed hashing

크기가 정해져있는 배열 내에 데이터를 저장함.
[용어 정리]
- k = key
- m = hash table의 크기
구체적인 응용 방법으로는 다음 세 가지가 있다.
- Linear probing
이미 그 자리에 데이터가 존재하는 경우, 오른쪽으로 한칸씩 이동하면서 빈칸을 찾아서 저장
i = 0, 1, 2, 3...일 때 h(i,k) = (h(k)+i) mod m
(mod m은 h(k)+i가 배열의 크기 넘어섰을 때 다시 0으로 돌아와서 빈칸 찾도록 하기 위함)



- Quadratic probing
바로 옆칸으로 계속 밀리는 게 아니라, 여러 칸을 건너뛰어서 저장. 데이터를 더 흩어놓을 수 있음.
i = 0, 1, 2, 3...일 때 h(i,k) = (h(k)+i²) mod m



- Double hashing
해쉬 함수를 하나 더 사용하는 방식. h₁(k)를 사용하고, 충돌시 h₂(k)를 사용.
i = 0, 1, 2, 3...일 때 h(i,k) = (h₁(k)+i*h₂(k)) mod m
=> 두 데이터가 h₁에서 동일한 값을 갖더라도, h₂에서 다른 값을 가지면 바로 빈칸을 찾아줄 수 있다.



그러나 이런 방법들은, 자료가 삭제될 경우 문제가 발생할 가능성이 있다!
ㆍclosed hashing에서, 자료가 삭제될 경우 문제점. (feat. linear probing)
h(a) = h(b) = 5라 하자.

같은 해쉬값을 갖는 a, b를 해쉬 테이블에 넣으려고 한다.

h(a) = 5번 인덱스에 a를 저장한다.

h(b) = 5번 인덱스에 b를 저장하려고 갔더니, 이미 a가 있다. 한칸 오른쪽으로 밀어서 저장한다.

a를 지우니 5번 인덱스 자리는 비어있다.

b를 검색하려고 봤더니, h(b) = 5번 인덱스에 아무것도 없다. 이게 원래 없었던 건지, 있었는데 지워진건지 모름.
따라서, a를 지우고 나서도 원래 뭐가 있었는지에 대한 정보를 보관하고 있어야 함!
◆ 단순한 형태의 해쉬 함수 - mod
간단한 해쉬함수를 생각해보자면,
해쉬 테이블의 크기가 m이라 할 때, h(k) = k mod m 의 형식으로도 만들 수 있다.
이때 m은 일반적으로 다음 두가지를 만족하는 m으로 설정함.
• 2^p or 10^p는 m으로 사용 안함. (각각 2진수, 10진수에서 k의 끝에서부터 p자리와 동일하기 때문)
• 2의 지수배가 아닌 prime number를 m으로 사용
(예) 다음 조건인 경우 mod를 사용한 해쉬 함수에서 m을 설정해보자.
- n = 2000
- data 하나는 8bits
- open hashing사용
- 평균 3번의 Unsuccessful Search 감수(검색 횟수의 평균을 3번으로 만들고 싶다)
이 경우, 다음과 같이 h(k)를 구성할 수 있다.
a = 2000/3
m = 701 (a에 가까우면서 2^p에 가깝지 않은 소수)
→ h(k) = k mod 701
◆ 선택 문제(selection problem)란?
키가 n개인 리스트에서 k번째로 큰(또는 작은) 키를 찾는 문제 (키가 정렬되어 있지 않다고 가정)
◆ 선택 문제(selection problem) - 최대(max)키 찾기
크기 n인 배열 S에서 최대키를 찾음. large 변수 사용
[pseudo code]
void find_largest(int n, const keytype S[], keytype& large){
index i;
large = S[1];
for (i=2; i<= n; i++)
if (S[i] > large) //S[i]와 large 비교해서, S[i]가 더 크면 large 업데이트
large = S[i];
}T(n)은 항상 n-1
키 비교만 수행하여, 가능한 모든 입력 n개 중에서 최대키를 찾을 수 있는 결정적 알고리즘은 어느 경우라도 반드시 최소한 n-1번의 비교를 해야 한다.
◆ 선택 문제(selection problem) - 최소키와 최대키 찾기
small, large 변수 사용
[pseudo code]
void find_both (int n, const keytype S[], keytype& small, keytype& large){
index i;
small = S[1];
large = S[1];
for (i=2; i<= n; i++)
if (S[i] < small) //S[i]와 small 비교해서, S[i]가 더 작으면 업데이트
small = S[i];
else if (S[i]> large) //앞 if문에 들어갔다면 여기로 못옴ㅇㅇ
large = S[i]; //S[i]와 large비교해서, S[i]가 더 크면 업데이트
}small쪽, large쪽 각각 n-1씩 걸리므로 W(n) = 2(n-1)
최악의 경우 : S[1]이 젤 작은 데이터인 경우. 항상 if문 비교 + else if문 비교까지 수행하기 때문 (if에 안들어가니까 항상 else if까지 봐야함)
◆ 선택 문제(selection problem) - 짝을 지어서 최소키와 최대키 찾기
인접한 두개끼리 짝을 지어서, 둘중 큰 값(Large)와 작은 값(Small) 나눠서 각각 L, S배열에 넣음

총 개수를 n이라 할 때, 총 3n/2 -2번 비교함. (step별로 합치면) => O(3n/2)
[pseudo code]
void find_both2t(int n, const keytype S[], keytype& small, keytype& large){
index i;
//초기 small, large값 지정
if (S[1] < S[2]) {
small = S[1];
large = S[2];
}
else {
small = S[2];
large = S[1];
}
//짝지어서 비교. (n-2)/2회 반복(초기화시 했던 비교 제외)
for (i=3; i<= n-1; i=i+2){
//경우1. 앞<뒤
if (S[i] < S[i+1]){
if ( S[i] < small)
small = S[i];
if ( S[i+1] > large)
large = S[i+1];
}
//경우2. 앞>=뒤
else {
if ( S[i+1] < small)
small = S[i+1];
if ( S[i] > large)
large = S[i];
}
}
}
for문 한번 반복할 때마다 3번 비교(if or else, if, if)하므로, T(n)은 다음과 같다.

◆ 결론
키를 비교만 해서 최대/최소키 찾는 경우,

?
◆ 차대키 (second largest key) 찾기
1. 단순한 방법
2. 토너먼트 방법
(단계1) 토너먼트를 시행하여 최대 우승자가 최대키이다.
(단계2) 각 시합의 진 팀을 이긴 팀의 리스트로 만든다.
(단계3) 우승팀의 리스트에서 최대값을 찾으면, 이것이 차대키이다.

여기서 우승팀(18)의 리스트는 [12, 16, 15].
지금까지 비교한 애들중 나보다 작은 애들을 의미.
이중 가장 큰 건 16이므로, 16이 차대키.
◆ 차대키 (second largest key) 찾기 - 시간 복잡도 분석
1. 총 시합 횟수
1단계: n/2
2단계: n/2²
3단계: n/2³
...

T(n) = n-1
2. 우승팀 리스트에서 차대키 찾기
최대키의 리스트 크기는 lg n. (리스트에는 총 비교 단계 수만큼 있는데, 한 단계마다 데이터가 절반씩 줄어들기 때문)
그러므로 리스트 중 최대값 찾기는 lg n – 1 시간.
합계:

결론:
키를 비교만 해서 모든 가능한 입력에서 n개의 키 가운데 차대키를 모두 찾을 수 있는 결정적 알고리즘은 최악의 경우 최소한 다음의 비교를 수행해야 한다.

◆ k번째 작은 키 찾기
정렬되지 않은 데이터에서, k번째 작은 키를 찾는 방법
(1) 단순방법
정렬 후 k번째 선택 – Θ(n lg n)
(2) partition 사용
selection(1,n,k)
✓ quick sort의 partition을 사용
✓ W(n) = n(n-1)/2, A(n) ≈ 3n
(3) O(n) 방법
◆ k번째 작은 키 찾기 - partition 사용
(2) partition 사용
selection(1,n,k)
✓ quick sort의 partition을 사용
✓ W(n) = n(n-1)/2, A(n) ≈ 3n

4번째 키 찾고싶으면 왼쪽, 8번째 키 찾고싶으면 오른쪽 파트 보면 됨
최악의 경우는, pivot point가 max 또는 min이어서 효율적으로 분리가 안된 경우(한쪽으로 쏠린 경우).
partition 안했을때랑 별 차이 없이 다 비교해야 하기 때문.
[pseudo code]
keytype selection(index low, index high, index k){ //k번째로 작은 수 찾기
index pivotpoint;
if (low == high) // 원소가 하나밖에 없는 경우
return S[low]; // 리턴
else { // 그렇지 않은 경우
partition (low, high, pivotpoint); // 파티션 한번 해줌
if(k==pivotpoint) //내가 찾으려는 k가 pivotpoint번째인 경우
return S[pivotpoint]; //해당 아이템 리턴
else if (k<pivotpoint) // k가 pivotpoint번째보다 더 작은 경우
return selection(low, pivotpoint-1,k); //low, pivotpoint-1로 재귀
else //k가 pivotpoint번째보다 더 큰 경우
return selection(pivotpoint+1, high, k); //pivotpoint+1, high로 재귀
}
}selection(1,n,k)
//partition()을 통해 pivotpoint의 적절한 위치를 잡아서 레퍼런스로 돌려줌
void partition (index low, index high, index& pivotpoint){
index i, j;
keytype pivotitem;
pivotitem = S[low]; // 맨 왼쪽에 있는 데이터를 pivotitem으로 설정
j = low; // j를 맨 왼쪽 데이터로 초기화. j는 잠재적 pivotpoint
for (i = low + 1; i <= high; i++){ // i는 젤 왼쪽 다음~ 젤 오른쪽까지
if (S[i] < pivotitem){ // S[i]가 현재 pivotitem보다 작으면,
j++; // j 하나 증가 (S[i] 들어갈 자리 하나 확보)
exchange S[i] and S[j]; //S[i] <-> S[j] 해서 S[i]를 앞쪽으로 옮김
}
} //j: pivotitem 보다 작은 그룹의 제일 우측 끝 데이터의 위치
pivotpoint = j; // 반환할 pivotpoint 인덱스 위치 설정
exchange S[low] and S[pivotpoint]; // 현재 pivotitem 값을 pivotpoint(올바른 위치임)에 넣어준다.
}
■ selection(1,n,k)의 시간 복잡도
n개의 데이터에서 k번째를 지정하면, k번째를 찾을 수 있는데 그것이 n에 대한 비례 시간으로 찾을 수 있다.
✓ 최악의 경우: pivotpoint의 데이터가 min 또는 max인 경우. 제대로 분리를 못하니까.
W(n) = n(n-1)/2
W(n) = W(n-1) + n-1
✓ 최선의 경우: pivotpoint의 데이터가 중간에 위치하는 경우
B(n) = 2n
B(n) = B(n/2) + n-1
✓ 평균의 경우:
A(n) ≈ 3n
◆ k번째 작은 키 찾기 - O(n) 방법
[pseudo code]
procedure SELECT(k,S) //전체 데이터 S중에서 k번째를 찾는다.
if |S| < 50 then //임계점. S가 50보다 작으면, (어느정도보다 작으면)
sort S // 정렬한 다음에 k번째를 찾아라.
return kth smallest element in S
else // 그렇지 않으면,
divide S into floor(|S|/5) sequences of 5 elements //S를 5개씩으로 분해
sort each 5-element sequence //분해한 애들 각각 정렬(O(n))
let M be the sequence of medians of the 5-element sets //각각 분해된 그룹에서 가운데 원소 하나씩 뽑아내서 M 만듦(M크기는 n/5이 될 것)
m ← SELECT(ceiling(|M|/2), M) //그렇게 만든 M중에 M/2번째 원소(가운데 원소)를 m이라고 하자 (T(n/5))
let S1, S2, and S3 be the sequences of elements in S //m기준으로 S를 세 그룹으로 나눔. (O(n))
(less than, equal to, and greater than m, respectively. //S1: m보다 작음, S2: m과 같음, S3: m보다 큼)
if |S1| ≥ k, //k가 S1번째보다 작은 경우, 즉 k가 S1그룹에 들어있는 경우에
then return SELECT(k,S1) //S1에서 k를 찾아보자!
else
if |S1| +|S2|≥ k, //k가 S1+S2번째보다 작은 경우, 즉 k가 S2그룹에 들어있는 경우
then return m //m의 값을 리턴하면 k값을 찾은 것임!
else //S2까지도 없으면, S3에서 찾아야함
return SELECT(k-|S1|-|S2|, S3) //k에서 S1, S2크기 빼야 S3내에서의 인덱스 찾을수있음
< 방법 >
1. 데이터를 5개의 묶음으로 만듦

2. 5개의 묶음 내에서 정렬

3. 5개의 묶음 각각의가운데 값들을 모아 M 생성

4. M에서 ceiling(|M|/2) 번째(가운데)를 찾음 : m ← SELECT(ceiling(|M|/2), M)

5. m보다 작은 데이터 S1, 같은 데이터 S2, 큰 데이터 S3를 생성

6.
if |S1| ≥ k, then return SELECT(k,S1)
else
if |S1| +|S2|≥ k, then return m
else return SELECT(k-|S1|-|S2|, S3)

7. 작아진 문제에 대해 select 수행
◆ k번째 작은 키 찾기 - O(n) 방법 - 시간 복잡도 분석
T(n) ≤ T(n/5) + T(3n/4) + cn

1. 5개로 나뉜 애들 다 정렬하는 시간 O(n)
2. 5개에서 하나씩 뽑은 애들 정렬하는 시간 T(n/5)
3. S를 m기준 S1, S2, S3로 분리하는 시간 O(n)
4. S1 또는 S3에서 찾는 시간 T(3n/4)
4를 좀 더 자세히 보자. S1과 S3의 크기의 상한에 대한 설명이다. m과 S1, S3 사이의 관계를 볼 것이다.
우선 과정 좀 더 자세히 보면!
1) 데이터를 5개의 묶음으로 만듦.

2) 5개의 묶음 내에서 정렬

3) 5개의 묶음의 가운데 값들을 이용하여 묶음 정렬

4) 묶음들을 재배치

이런 식으로 이루어진다.
다음 그림을 보자.

실제로 데이터가 정렬되어 있지는 않지만, 관계를 파악하기 위해서 가로, 세로로 그림과 같이 정렬되어 있다고 가정하자.
이때, m을 기준으로 한 확실히 m과 같거나 작은 영역, 확실히 m과 같거나 큰 영역의 분포는 위와 같다.
전체 데이터 개수를 n이라고 하면, 그중 m이 있는 라인의 데이터들의 개수(중앙값 하나씩 뽑아온 그룹)는 n/5이고,
그중에서 m이 중앙값이다. 따라서 m의 그룹 내에서 m보다 같거나 큰 데이터와 같거나 작은 데이터 모두 n/10개가 된다.
m그룹 밖까지 생각해보면, m보다 무조건 같거나 작은 데이터나 m보다 무조건 같거나 큰 데이터의 개수를 구할 수 있다.
- m보다 무조건 같거나 작은 데이터의 경우 n/10개가 2번 더 존재한다.(각각 가져온 중앙값보다 작았던 애들)
- m보다 무조건 같거나 큰 데이터 역시 n/10개가 2번 더 존재한다.(각각 가져운 중앙값보다 컸던 애들)
따라서, m보다 무조건 같거나 작은 데이터는 3n/10이고, m보다 무조건 같거나 큰 데이터도 3n/10개 이다.
- m보다 작을수도 있는 데이터를 구하기 위해서는, n - m보다 무조건 같거나 큰 데이터 = n - 3n/10 = 3n/4개 이고,
- m보다 클수도 있는 데이터를 구하기 위해서는, n - m보다 무조건 같거나 작은 데이터 = n - 3n/10 = 3n/4개 이다.
▶ 실제 데이터를 넣어서 보면 이렇다~
색칠되어있지 않은 영역은 m보다 클 가능성도, 작을 가능성도 있는 영역을 의미한다.
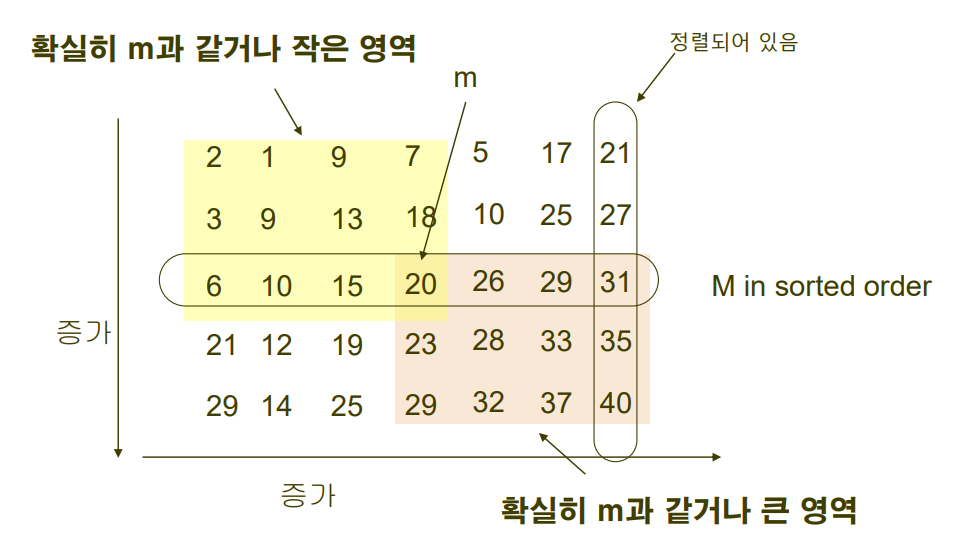
m보다 작을 수 있는 영역은 회색 + 흰 영역 (3/4)이고, m보다 클 수 있는 영역은 주황 영역 + 흰 영역(3/4)이다.
따라서 S1과 S3는 최대 3n/4개씩 존재할 수 있다.

※ Selection vs Select
✓ selection( ) - 단순 partition을 사용할 경우
- 임의의 pivotitem을 선정
✓ select( ) - median of median 방법(중앙값들의 중앙값)
- 한 쪽의 데이터 개수를 3n/4 으로 한정(최악의 경우를 개선했다! 는 의의)
◆ 문자열 매칭
입력 문자열에서 패턴을 찾는 문제.
즉, ctrl+f 누르면 나오는 찾기 기능 구현에 관한 이야기.
1. 원시적인 매칭 방법
2. 오토마타를 이용한 방법(컴파일러 구조)
3. Rabin-Karp 알고리즘
4. Boyer-Moore 알고리즘

그림과 같이, 입력 문자열 A[1...n]이 있고 그 안에서 패턴 p[1...m]을 찾고자 한다. (m<<n)
◆ 문자열 매칭 - 원시적인 매칭 방법(기본적인 방법)
처음부터 끝까지 한 char씩 이동하면서 비교한다.

[pseudo code]
naiveMatching(A,p) { //문자열 A와 입력 패턴 p
for i=1 to n-m+1 { //A의 길이 n에서 p의 length m 뺀 만큼 + 1 (n=10, m=4면 7까지는 비교해야함)
if (p[1..m]==A[i..i+m-1]) //한 char씩 비교. 최대 m번째까지 비교: O(m)
matching is found at A[i] //m개의 char이 다 동일하다면 매칭 성공
}
한칸씩 옮기면서 n-m+1번 비교하고, 한번 비교할 때마다 최대 m개씩 비교하기 때문에 O(mn)
◆ 문자열 매칭 - 오토마타(automata)를 이용한 방법
컴파일러에서 나오는 내용.
- 상태 전이 함수 δ를 이용한 방법
- 어휘분석 단계에서 오토마타가 쓰임.
- state transition diagram

프로그램에서 사용하는 identifier가 있으면, 이 identifier를 인식하는 상태전이 다이어그램임.
시작하면, S와 A는 상태를 구분하기 위한 내용.
◎ 표시는 Final State: 정상적으로 인식했을 때 이 상태에 있으면 제대로 인식된다는 의미.
위의 상태전이도에서 identifier는 첫 character가 알파벳(letter)이고, 그 다음은 알파벳 또는 digit이 온다고 했을 때의 상태전이도인 것. (a123, aa12, bear, oh10..는 매칭 되지만, 1a23, 324m, .. 같이 숫자로 시작하는 건 매칭 안됨)
[pseudo code]
FiniteAutomataMatcher(A,δ,f) {//f: final state
q = 0; // 처음 상태
for i=1 to n { //i는 1부터 n까지
q = δ(q, A[i]); //현재 상태에서 i번째 character을 받아들여서 만들어진 새로운 상태를 q라 하자
if (q=f) // 만약 새 q가 final state라면,
matching is found at A[i-m+1] // A[i-m+1]에서 매칭 성공
}i가 1부터 n까지 돌기 때문에, 시간 복잡도는 Θ(n)
예시) 정수를 인식하는 상태전이도 ?
인식하는 형태: 10진수, 8진수, 16진수로 구분되어진다.
- 10진수 : 0이 아닌 수로 시작
- 8진수 : 0으로 시작
- 16진수 : 0x, 0X 시작

여기서 123a가 int로 인식이 되는지?
=> 123까지는 A state로 넘어가지만, a가 들어오면 더이상 상태 전이를 못하므로 int로 인식 못한다.
예시) 실수를 인식하는 상태전이도
인식하는 형태: Fixed-point number, Floating-point number

- e: exponent(거듭제곱)
- d: decimal(십진법)
=> 3.0, 3.4, ...이 들어오면 C에서 종료.(실수로 인식함)
=> 2나 a가 들어오면 실수로 인식 못함
◆ 문자열 매칭 - Rabin-Karp 알고리즘
- 문자열 패턴을 숫자로 바꾸어, 숫자 비교를 통해 패턴을 찾음

- [팔오육일]이라는 패턴을 [팔천오백육십일]로 변환해서 비교해서 패턴을 찾는 느낌
- v = 1+10ⅹ6+10²ⅹ5+10³ⅹ8
그런데 이렇게 연산하면, 10의 n승을 계속 구해야 하므로, 다음과 같이 연쇄적으로 계산한다. (곱셈 줄일 수 있음)
- v = 1+10ⅹ(6+10ⅹ(5+10ⅹ8))
일반화해서 표시하면 다음과 같다.
- 패턴 p[1..m]이 10진수 이면
v = p[m]+10ⅹp[m-1]+10²ⅹp[m-2]+…+10m-1ⅹp[1]
= p[m]+10ⅹ(p[m-1]+10ⅹ(p[m-2]+…+10ⅹp[1]))..)
▪ 문자열 A[i,..,i+m-1]의 값, 즉 문자열 A에서 i번째~ i+m-1번째의 데이터를 이용한 값은 다음과 같이 표현된다.
A[i+m-1]+10ⅹ(A[i+m-2]+10ⅹ(A[i+m-3]+…+10ⅹA[i]))..)

▪ ai 계산은 Θ(m) 필요 (총 m자릿수만큼 비교해야 함)
• 입력 문자열에 대해 처음 m개의 문자별로 ai를 계산하면 됨.

▪ 총 계산 횟수는 n-m+1번 (i=1 부터 n-m+1).
▪ 따라서 i를 변경하면서, ai 값과 v를 비교하면 총 수행시간은 Θ(mn)
▪ 문제점: 패턴의 길이만큼 연산해서 숫자로 변환해야 하기 때문에 계산값이 커진다.
※ d는 다른 base를 사용 가능(문자를 d 진수로 표현한 경우, 10을 d로 변경.)
■ 개선 방안1
매번 모든 계산을 해야 하는 것은 아니다!
겹치는 자릿수는 이전 a에서 가져와서 쓸 수 있음.
ai 계산시 ai-1 이용
ai = A[i+m-1]+10ⅹ(A[i+m-2]+10ⅹ(A[i+m-3]+…+10ⅹA[i])))
= 10ⅹ(ai-1 - 10m-1ⅹA[i-1]) + A[i+m-1]
ex)

a₁= 529 라 할 때, 다음과 같은 방식으로 a₂를 구한다.
a₂= 10ⅹ(529-102ⅹ5)+4 = 294
• 이 방식으로는 한번의 a값을 계산하는데 곱셈 2회, 덧셈 2회 필요
• n-m+1 반복, m≪n
• 총 Θ(n)
• 문제점: 이 방법 역시, 계산값이 너무 커질 수 있다.
[pseudo code]
basicRabinKarp {
v ← 0; a_1 ← 0; //d 진수
for i=1 to m //i가 1부터 v의 length만큼
v = dⅹv + p[i]; //v값 계산
a_1 = dⅹa_1 + A[i] //a1값(초기 a값) 계산
for i=1 to n-m+1 //i가 1부터 length(A)-length(v)+1까지
if(i≠1) //아까 초기 a는 계산했으므로, 다음으로 넘기지 않고 뒤에서 v와 비교부터 해야함
a_i ← dⅹ(a_i-1 - dm-1ⅹA[i-1]) + A[i+m-1] //이전 a로부터 현재 a 계산
if(v = a_i) //v와 현재 a비교. 같을 시 매칭 성공
matching is found at i
}■ 개선 방안2
mod 함수를 이용해 큰 값이 나오지 않도록 하는 방법.
- q: prime number(소수)를 사용
- d: d진수를 의미
d×q 가 컴퓨터가 처리 가능한 범위가 되도록 q 설정
a_i 대신 b_i = a_i mod q 사용
- 기존 a_i = 10ⅹ(a_i-1 - 10m-1ⅹA[i-1]) + A[i+m-1]
- b_i = (dⅹ(b_i-1- (d^m-1 mod q)ⅹA[i-1]) + A[i+m-1]) mod q
이때 d^m-1 mod q는 미리 계산해서 활용함.
ex)

[pseudo code]
RabinKarp {
v ← 0; b1 ← 0; //d 진수
for i=1 to m { // i는 1부터 length(v)까지
v = (dⅹv + p[i]) mod q; // v계산
b_1 = (dⅹb_1 + A[i]) mod q // b1(초기 b) 계산
}
h = d^(m-1) mod q //항상 일정하게 쓰이는 값이므로 저장해둠
for i=1 to n-m+1{ //i는 1부터 length(A)-length(v)+1까지
if(i≠1) //아까 초기 a는 계산했으므로, 다음으로 넘기지 않고 뒤에서 v와 비교부터 해야함
b_i ← (dⅹ(b_i-1 - hⅹA[i-1]) + A[i+m-1]) mod q
if(v == b_i){ // 같은 값이면 매칭이 실제 되는지 확인해야 함(실제론 다른데 mod값만 같을수도 있음)
if(p[1..m] == A[i..i+m-1]) matching is found at i
}
}
}✓ bi 계산에 2회 곱셈, 2회 덧셈. mod 1회
✓ 전체 비교 루프는 n-m+1 반복 → 총 Θ(n)
✓ 매칭확인 시간(일단 mod값은 같은 경우) → 패턴의 길이만큼 반복하므로 Θ(m) (mod 계산에 의해 패턴이 다른 데이터에서 매칭이 일어날 수 있다)
✓ 총 k번의 매칭 확인이 필요하다면, 총 Θ(n + km)
✓ 충분히 큰 q>n 일 때 false matching(mod값은 같지만 매칭은 안된 경우)은 1회 미만.
결론: Θ(n)
◆ 문자열 매칭 - Boyer-Moore 알고리즘
패턴의 끝에서부터 비교하는 방법.
Boyer-Moore의 약식 알고리즘(단순 형태)인 Boyer-Moore-Horspool 알고리즘에 다뤄볼 것.

✓ (1)에서 A[1] ≠ p[1] (t ≠ b)일 때 단순한 방법에서는 (2)로 이동
✓ 만일 (1)에서 A[4]≠p[4] 를 먼저 확인한다면, (1)에서 (3)으로 이동 가능(Boyer-Moore-Horspool)
왜냐하면 A[4]=h가 패턴 내에 아예 없기 때문임!
✓ 만일 패턴이 ‘show’ 라면 (4)에서 비교해 본 후, 다음에는 (5)로 이동. 6번째 칸(b와 w)부터 확인 시작.
✓ 패턴의 제일 뒤(오른쪽) 부터 검사 => 일치하지 않을 때 여러 칸을 jump해서 이동 가능
ex)
다음은 매칭 실패시 이동 거리 표이다. (패턴의 정보를 이용해 만들면 됨)

오른쪽 끝 문자라는 것은 입력 문자열의 현재 매칭 확인하는 구역의 오른쪽 끝 문자를 의미함.

오른쪽 끝 문자인 h와 패턴의 끝 문자인 t를 비교를 비교했더니 일치하지 않음.
따라서 표에 따라 etc에 해당하는 4칸을 이동할 수 있음.

오른쪽 끝 문자인 h와 패턴의 끝 문자인 t를 비교를 비교했더니 일치하지 않음.
따라서 표에 따라 o에 해당하는 2칸을 이동할 수 있음.
■ 단순한 방법 vs Boyer-Moore-Horspool 방법
[pseudo code]
// 단순한 방법
naiveMatching(A,p) {
i = 1;
while(i ≤ n-m+1) {
if(p[1..m] == A[i..i+m-1])
a matching is found at A[i]
i=i+1
}
}
[pseudo code]
// Boyer-Moore-Horspool 방법
BoyerMooreHorspool(A,p) {
computeJump(p, jump);
i = 1; //i는 A내 위치에 대한 인덱스
while(i ≤ n-m+1) { // 한번에 여러 char을 점프할 수도 있으므로, for이 아닌 while로 정의
j = m; //j는 패턴의 마지막 문자
k=i+m-1; //k는 이번 비교에서의 오른쪽 끝 문자
while(j>0 and p[j]==A[k]){ //p와 이번 A가 같은지 뒤에서부터 확인(다르면 바로 탈출)
j--;
k--;
}
if(j==0) //첫번째 j까지 비교하고 탈출했다면 매칭된 것
a matching is found at A[i]
i= i + jump[A[i+m-1]]; //그렇지 않다면 표에서 오른쪽 끝 문자에 해당하는 점프 횟수만큼 찾아서 점프
}
}
■ 그러면 jump 정보 표는 어떻게 작성하느냐!
보통은, 다음과 같이 length-1부터 1씩 감소하면서 적어줌

만약 패턴 안에 중복이 있을 경우, 더 작은 값으로 적어줌(큰 값으로 이동했다가는 과하게 이동할 수 있음)

✓ 같은 문자가 있을 경우는 작은 jump 값으로 설정
✓ 총 매칭 시간: O(mn). 그렇지만, 점프를 크게크게 하기 때문에 A의 길이인 n만큼 다 보지는 않고 빨리 진행됨
✓ Boyer-Moore 방법은 이 방법보다 정교한 jump 판단 방식채용
'CS > 알고릴라' 카테고리의 다른 글
| 7장. 계산복잡도의 소개: 정렬 문제 (0) | 2023.05.30 |
|---|---|
| 6장. 분기 한정법(Branch-and-Bound) (0) | 2023.05.18 |
| 5장. 되추적 (Back-tracking) (0) | 2023.05.16 |
| 4장. 탐욕적인 접근방법(Greedy Algorithm) (2) (0) | 2023.05.01 |
| 4장. 탐욕적인 접근방법 (Greedy Algorithm) (1) (0) | 2023.04.17 |




