센로그
4장. 탐욕적인 접근방법(Greedy Algorithm) (2) 본문
◆ Dijkstra 알고리즘
하나의 출발 지점으로부터 다른 모든 도착 지점들로 가는 각 최단 경로들을 모두 계산할 때 쓰는 방법
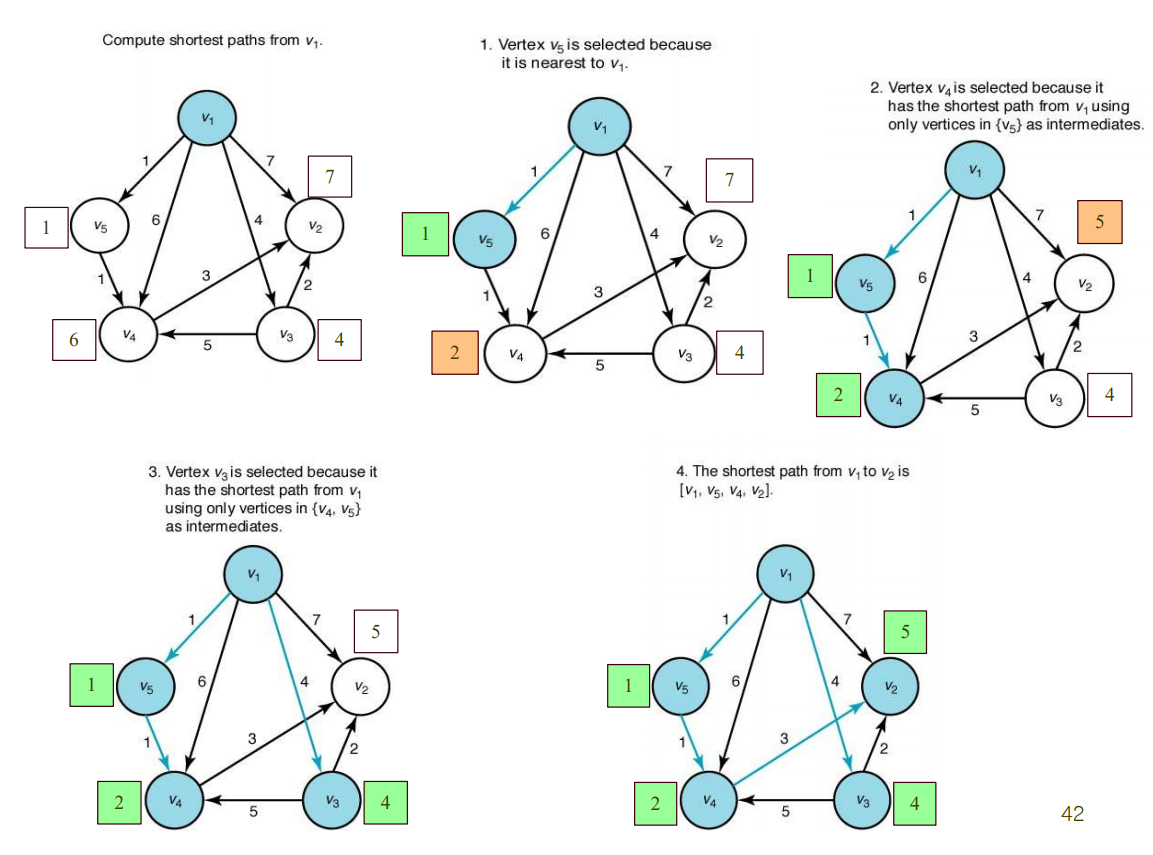
< 방법 >
- F (최종 결과 엣지 집합)를 공집합으로 초기화
- Y (최단 경로가 확정된 노드들 집합)는 출발 노드로 초기화.(예시에서는 v1에서 출발하는 걸로 가정)
- V-Y집합(최단 경로가 확정된 노드들을 제외한 노드들)에 속한 노드 중에서, v1(출발 노드)에서 Y에 속한 정점만을 거쳐서(무조건 거쳐야 하는 것은 아님) 최단 경로가 되는 정점 v를 선정한다.
- 그 정점 v를 Y에 추가한다.
- v에서 Y로 이어지는 엣지('v와 Y를 잇기 위해 Y내에서 최종 경유하는 노드'와 'v노드'간의 엣지)를 F에 추가한다.
- Y = V가 되면(전체 노드 다 돌음), T = (V, F)가 최단 경로를 나타내는 그래프(vertices, edges)
[pseudo code]
void dijkstra(int n, const number W[][],set_of_edges& F) { //노드 수, 가중치 배열, 반환할 F
index i, vnear;
edge e;
index touch[2..n]; // v1에서 시작해서, (V-Y에 속하는)vi까지 최단 거리로 갈 때,
// Y내에서 최종적으로 경유하는 노드의 index
// 시작노드가 v1이라 가정했으므로 2부터 시작
number length[2..n]; // v1에서 시작해서, (V-Y에 속하는)vi까지의 최단 거리
// 초기화
F = ϕ;
for(i=2; i <= n; i++) { // 첫 노드를 v1으로 잡고, touch[]와 length[] 초기화
touch[i] = 1; // 처음엔 Y에 v1밖에 없으므로, 모든 노드에 대한 touch[i] = 1로 초기화
length[i] = W[1][i]; // 처음엔 Y에 v1밖에 없으므로, v1과 vi를 직접 잇는 엣지의 가중치로 초기화
}
repeat(n-1 times) { // 처음 Y에 추가한 1을 제외하고 n-1번 반복(반복시마다 한 노드확정)
// Y에 속한 노드와 가장 가까운 V-Y의 노드인 vnear 찾기
min = ∞;
for(i=2; i <= n; i++) // 각 정점들에 대해서
if (0 <= length[i] < min) { // 출발 노드 v1과, (V-Y에 속한) vi 사이의 가중치가 min보다 작은 경우
// 이때, 이미 Y에 속하는 노드(length[i] > 0인 경우)는 제외
min = length[i]; // min 업데이트
vnear = i; // 그 노드의 index로 vnear을 업데이트
}
e = (touch[vnear], vnear); // vnear과 touch[vnear]을 잇는 엣지
e를 F에 추가;
// 업데이트된 Y에서, v1과 (V-Y에 속한) vi사이의 length가 감소할 수 있는지 확인
for(i=2; i <= n; i++)
if (length[vnear]+ W[vnear][i] < length[i]) { // v1~vnear + vnear~vi의 거리가 기존 v1~vi의 거리보다 작다면
// 이때, 이미 Y에 속하는 노드까지의 length는 -1이므로 여기 안들어감
length[i] = length[vnear] + W[vnear][i]; // length[i]를 갱신한다
touch[i] = vnear; // 이에 따른 touch[i]도 갱신
}
length[vnear]=-1; // 찾은 노드를 Y에 추가한다.
}
}

◇ Dijkstra 알고리즘 - 시간 복잡도 분석

(n-1) 반복 안에, 두번의 (n-1) 반복문이 있으므로 (n-1) * 2(n-1) = 2(n-1)²
따라서 T(n) = 2(n-1)² ∈ Θ(n²)
근데.. heap으로 구현하면 Θ(m lg n)까지 줄일 수 있다고 한다!
◆ Dijkstra 알고리즘 - heap으로 구현
start부터 node까지의 length가 현재보다 작은 node에 관한 정보를 최소 heap에 담아두고 작은거부터 꺼냄
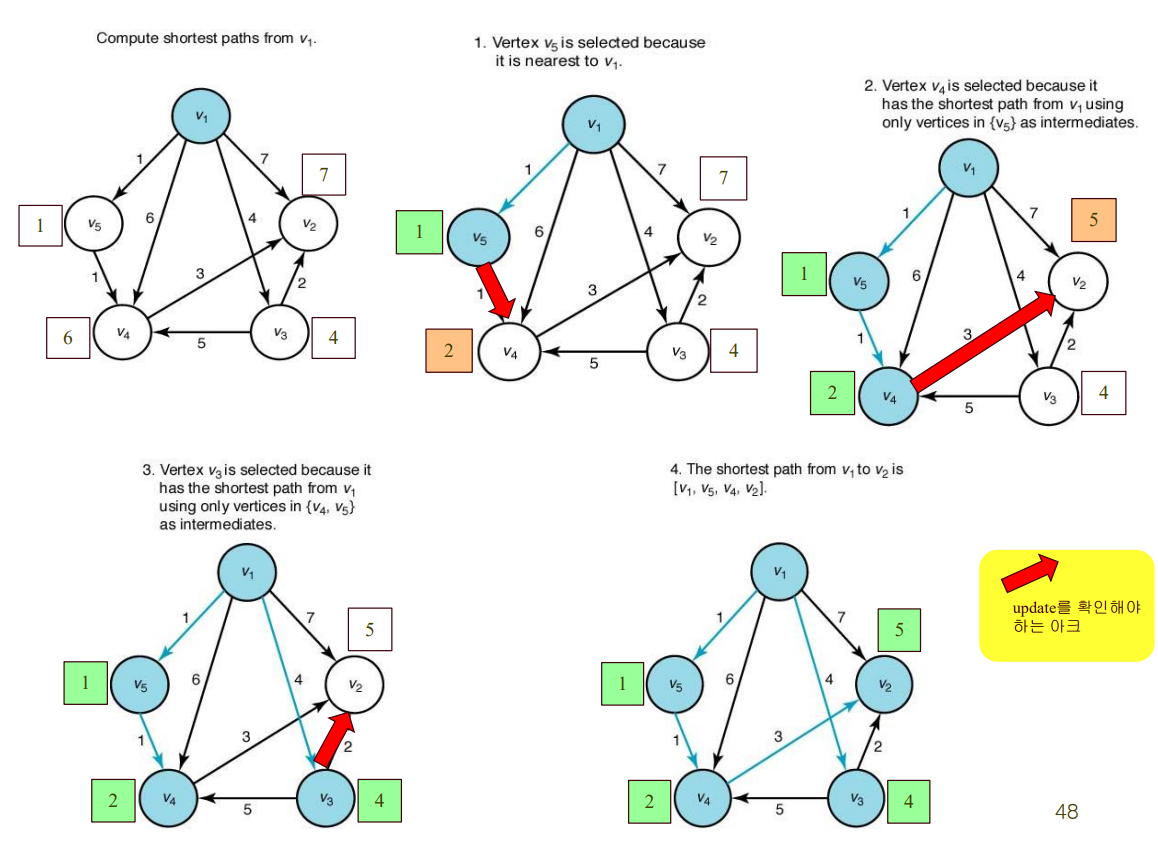
빨간 화살표로 확인한 엣지는, 한번 확인하고 다시는 확인 안해도 되는 엣지임.
< Heap(pq)으로 구현 >
- 방문하지 않은 노드 중에서, length가 현재보다 작은 node에 관한 정보를 pq에 담아둠
- 위에서부터 하나씩 꺼내서 갖고옴. 이때, 그 노드 차례가 되기 전(아직 방문하기 전)까지는 그 노드 정보가 추가로 pq에 저장될 수도 있음. 그러다가 만약 그 노드를 이미 처리했으면, 그 다음에 다시 나오는 해당 노드 정보는 안봐도 됨.
length와 touch 업데이트 확인 시, 굳이 다 반복하며 확인하지 않고 필요한 횟수만큼만 확인하는 것.=> 우선순위 큐
< 시간 복잡도 >


- O(n lg n) : root에서 min을 갖고 오고(n번), Heap을 재정렬하는 시간(log n 시간)
- m : 총 엣지수 - v1에 연결된 엣지 수
- length와 touch 업데이트 확인 시, 한번 안 고른 엣지는 다음에 다시 확인 안해도 됨. (이미 한번 안고를 때, 걔보다는 좋은 경로가 있는 것이 확정된 셈이니까).
=> 즉, 전체 알고리즘에서 하나의 엣지는 한번만 확인해주면 되는 것! 따라서 애초부터 v1에 연결되어 있던 애들(length 초기화시 미리 넣어둠)을 제외한 엣지들을 확인해주면 된다.
=> m번 만큼 heap operation을 해주면 되는데, 데이터 개수가 n개인 heap operation은 log n 시간이 소요되므로 Θ(m lg n)
따라서 총 시간복잡도는 O(n lg n) + Θ(m lg n)인데, m ≥ n이므로 Θ(m lg n)
참고) Heap 연산에서의 시간 복잡도

- 루트를 찾는 것 : O(1)
- 루트 찾고 재정렬 : O(lg n)
- 추가, 삭제, 수정 : O(lg n)
(최적여부 검증은 생략)
◆ Huffman Code
허프만 코드 자체가 아닌, greedy 알고리즘을 어떻게 적용해서 허프만 코드를 만들 수 있는지를 살펴볼 것임
허프만코드는 주어진 문자로 전치코드이자 최적 이진 코드를 만듦
- Fixed-length binary code
코드 길이가 고정.. but, 코드 빈도가 높더라도 같은 길이를 써야하므로 낭비가 생길 수 있음 - Variable-length binary code
코드의 길이가 변함.. but, 코드 길이가 다르므로 어디까지가 한 코든지 구분하기 힘들 수 있음(구분자 필요) - 최적 이진 코드: Optimal binary code
주어진 파일에 있는 문자들을 이진코드로 표현하는데 필요한 비트의 개수(총 비트수)가 최소가 되는 코드 - 전치코드: prefix code
한 문자의 코드워드가 다른 문자의 코드워드의 앞부분이 될 수 없도록 한 것(구분자 없어도 됨)
예시)

총 비트수
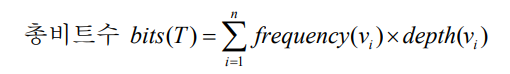
Σ(vi가 나타날 빈도수 * 트리에서 vi의 depth)
트리 구조상, vi의 depth가 vi의 코드 길이가 됨 ㅇㅇ
근데 같은 prefix 코드여도 최적이 될 수도 있고 아닐 수도 있기 때문에, 최적을 찾아야함 => greedy 적용해보자!
◇ 허프만 코드 구축 과정 - Greedy 알고리즘 사용

(0) 빈도수를 데이터로 갖는 n개의 노드를 생성
(1)~(5) 빈도수의 합이 최소가 되는 두 노드를 merge 시켜 이진트리로 구축(merge된 노드도 하나의 노드로 취급)
- 모든 노드가 하나의 이진트리가 될 때까지 반복
◇ 허프만 코드 구축과정 - 구현
PQ(min heap)에서 루트 빼서 p에 넣고, 루트 빼서 q에 넣음. 둘이 합친 r 만들어서 다시 PQ에 넣음. n-1번 반복!
< 준비물 >
우선순위 큐 - Heap (MinHeap)
노드타입 자료구조는 다음과 같이 설계할 수 있다.
struct nodetype {
char symbol; //문자
int frequency; //빈도수
nodetype* left;
nodetype* right;
};
[허프만 코드 생성 알고리즘]
for (i=1;i <= n-1; i++) { // 반복할 때마다 두개의 트리가 합쳐서 한 트리가 만들어지므로 n-1번
remove(PQ,p); // PQ에서 빈도가 제일 낮은 애를 빼서 p로 받음
remove(PQ,q); // 그 다음으로 빈도가 낮은 애를 빼서 q로 받음
// p,q를 합친 트리 r을 만듦
r = new nodetype;
r->left = p;
r->right = q;
r->frequency = p->frequency + q->frequency; // r의 빈도는 p빈도 + q빈도
// PQ에다 p와 q를 합친 r을 집어넣음
insert(PQ,r);
}
remove(PQ,r); //PQ에서 최종으로 합쳐진 하나를 빼서 r로 받아서 리턴
return r;빈도수가 작을수록 우선순위가 높다 (<= min heap은 빈도수가 작은 것부터 빼냄. 따라서 먼저 합치게 돼서, 최종적으로 아래쪽에 위치하게 됨)
실습해보기.
한번 조작할 때마다 lg n 만큼의 시간(heap operation)이 필요하기 때문에, 이를 n번 반복하면
Θ(n lg n) 이다.
◆ 0-1 Knapsack Problem (zero-one 배낭 문제)
어떤 물건을 넣느냐(1)/안 넣느냐(0)의 문제 (나눠서 넣을 수는 없음)
탐욕적 방법으로는 풀 수 없다
가장 가치가 크면서, 최대 무게를 초과하지 않도록 하는 것
- S = item들의 집합
- w_i = item_i의 무게
- p_i = item_i의 가치
- W = 배낭에 넣을 수 있는 최대 무게
라고 할 때,

한정된 무게 W 안에서 최대한의 가치를 갖도록 item을 넣는 방법
◇ 0-1 Knapsack Problem - 무작정 알고리즘
하나하나 다 고려해보자!
물건 개수가 n개일 때, 가능한 멱집합의 가짓수는 2ⁿ개이다. 넘 많음 ㅡ.ㅡ
◇ 0-1 Knapsack Problem - 탐욕적 알고리즘
우선 결론 : Greedy를 적용할 수 없는 문제다
가장 가치가 큰 물건부터 채워도 최적이 아니고, 가장 가벼운 물건부터 채워도 최적이 아니기 때문.
또, 무게당 가치가 가장 높은 물건부터 채워도 최적이 아님.
참고※ 배낭 빈틈없이 채우기 문제 (fractional kanpack problem)에서는 사용 가능함
문제를 잘라서 담을 수 있다는 가정 하에, 무게 한도 내에서 가장 큰 가치를 담을 수 있도록 하는 것!
→ 단위 무게당 가치가 큰 것부터 넣고, 더이상 넣을 수 없으면 배낭에 남은 무게만큼 잘라서 넣으면 됨.
◇ 0-1 Knapsack Problem - 동적 계획법
P[i][w] 배열을 채워넣으며, 최종적으로 P[n][W]의 값을 구하는 것이 목표.

P[i][w] = i번째 아이템까지 고려했을 때, 전체 무게가 w가 넘지 않는 한에서 최고의 이익
- i번째 아이템이 w보다 크다면, 아예 넣을수가 없는 것이므로 이번 턴 패스.
- i번째 아이템이 w보다 작거나 같다면, 최대 가치는 저번 턴(i-1 턴)의 최대 가치 또는 i번째 아이템을 포함했을 때의 가치 중 최댓값이다.(i번째를 포함하는 경우, i번째 아이템의 가치인 p_i를 더하고, 이번 턴 한도 무게에서 i번째 아이템의 무게인 w_i를 뺐을 때의 무게가 한도 무게였 때의 최대 가치를 더한 값이다.)
※ P[0][w] = 0이고, P[w][0] = 0 이다.
(0번째 아이템까지의 최고 이익은 0이고, 총 무게가 0을 넘지 않는 한에서 최고 이익도 0이다.)
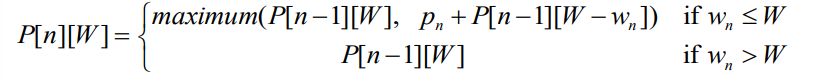
P[n][W] = 모든 아이템(n개)까지 고려했을 때, 전체 무게가 한도 무게(W)를 넘지 않는 한에서 최고의 이익
이게 바로 우리가 최종적으로 구해야 할 것!!
[pseudo code]
knapsack(p,w,n,W) { #p[], w[], n, W[][]
for(w=0 to W) P[0,w]=0 # 0번째 아이템까지의 가치는 0
for(i=0 to n) P[i,0]=0 # 총 무게가 0일때 까지의 가치는 0
for(i=1 to n) # 첫번째 부터 마지막 아이템까지
for(w=0 to W) # 무게가 0일때부터 최대 한도 무게까지 설정
if(w_i ≤ w) # i번째 아이템의 무게가 이번 루프에 설정한 최대 무게 이하일때
P[i,w] = max { P[i-1, w], p_i+P[i-1, w- wi]} # 넣/말 결정
else # 이번 루프에 설정한 최대 무게보다 크면
P[i,w] = P[i-1, w]; # 못 넣음
return P[n,W]
}
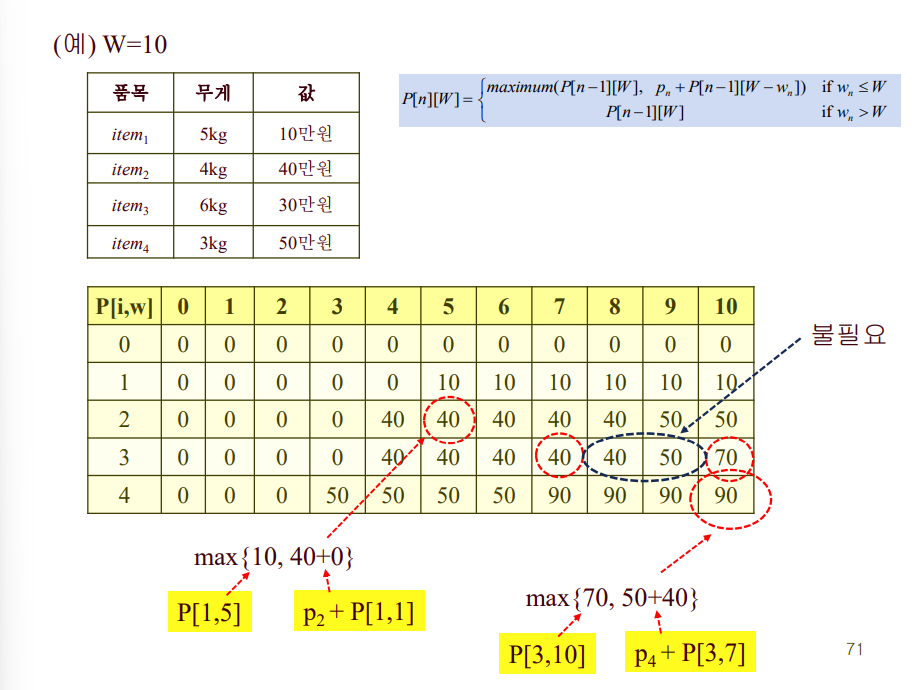
1행 1열은 다 0으로 초기화하고, 가로로 한줄씩 채움.
시간 복잡도는 Θ(nW)
근데 사실.. 만약 W가 n! 정도의 값을 가진다면, 무작정 알고리즘에 비해 하나도 나은 게 없음! ㅠㅠ
◇ 0-1 Knapsack Problem - 개선된 동적 계획법
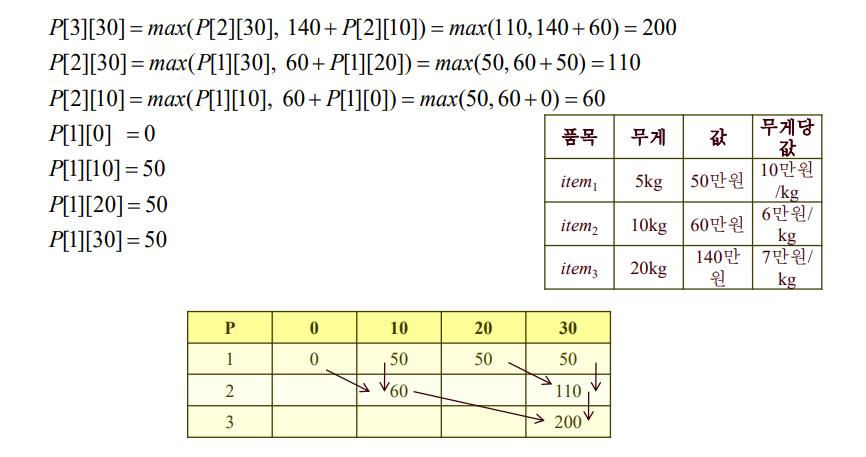
아이디어 : 모든 n-1 번째 행을 계산할 필요는 없다!
P[n-1][W]와 P[n-1][W-w_n] 식에 포함된 애들만 계산하면 됨
P[n-1][W]와 P[n-1][W-w_n] 식에 포함된 애들만 계산하면 됨.(재귀적으로 ㅇㅇ)
◇ 0-1 Knapsack Problem - 개선된 동적 계획법 시간복잡도
다음 두가지 경우 중 최악의 경우를 선정할 수 있다.
1) 한 턴을 계산하기 위해 2개의 이전 턴이 필요함.
n번째 턴을 계산하기 위해서는 2ⁿ-1개의 항을 계산해야 함!(등비급수 1+2+2²+...+2^(n-1)의 합)
따라서 Θ(2ⁿ)이다.
2) n=W+1이라고 하자. 모든 w_i가 1이라 하면(모든 아이템의 무게가 1), 한 턴을 계산할 때 고작 바로 붙어있는 대각선에서 갖고 오기 때문에, W 길이만큼 다 계산해봐야함. 따라서 1+2+3+...+n = n(n+1)/2 = (W+1)(n+1)/2 ∈ Θ(nW) 이다.
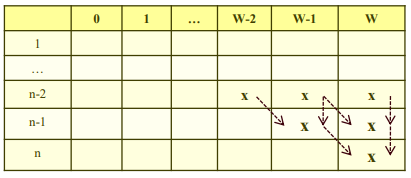
따라서, 최악의 경우 수행시간은
O(min(2ⁿ, nW))이다.
◆ 상호 배타적(Disjoint; 교집합이 공집합인.) 집합의 처리
상호 배타적: 서로 겹치는 원소가 없는.
프로그램 내에서 집합을 어떻게 표현하는 것이 좋은가? 표현 방법에 따라서 집합에 대한 연산 시간이 얼마나 걸릴것인가?
집합을 나타내는 세 가지 방법!
- linked list
- array
- tree
- 단순 방법
- 무게(weight) 고려 방법
- path compression(경로 압축) 방법
▶ 우리의 목표 : find(원소 찾기), union(집합 합치기)의 명령어가 다수 있을 때 효율적인 처리가 가능한 자료구조와 알고리즘을 찾는다.
1) linked list 사용
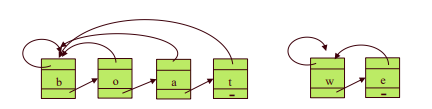
Operation
✓ make_set(v): v를 원소로 하는 집합을 만듦
✓ find(v): v가 속해있는 집합 이름(최초 원소값) 반환
✓ union(u,v): 원소 u와 원소 v를 갖고 있는 집합을 하나로 합친다. (u가 속해있는 집합 이름을 가리키는 포인터들을 v가 속해있는 집합 이름을 가리키도록 바꿔준다) 이미같은 집합에 속해 있을 수 있다.

근데 무작정 이렇게하면.. 크기가 큰 리스트가 작은 리스트로 옮겨 붙는 경우가 나올텐데, 넘 비효율적임.
최악의 경우: 총 n개의 원소가 있을 때, m번의 union은 최대 O(m²)소요 (m<n)
(1개를 1개에 붙이고, 2개를 1개에 붙이고, 3개를 1개에 붙이고... m개를 1개에 붙이는 경우)
=> 개선 : 리스트의 크기를 별도로 저장하고, 크기가 작은 리스트를 큰 리스트에 연결! (weighting-union heuristic)
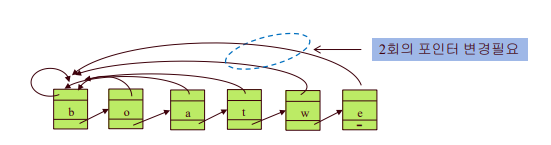
n개의 원소가 있을 때, 개선된 방법(weighting-union heuristic)으로 n-1번의 union을 수행하는 데 O(n lg n) step이 소요된다.
증명: 두 집합의 원소의 개수를 각각 A, B라 하자.
A < B일 때 A+B ≥ 2A 이기 때문. 한번 합칠 때 마다 집합 크기가 두배 이상씩 커짐!
따라서 어떤 원소도 lg n 번보다 더 많이 이동할 수 없음.
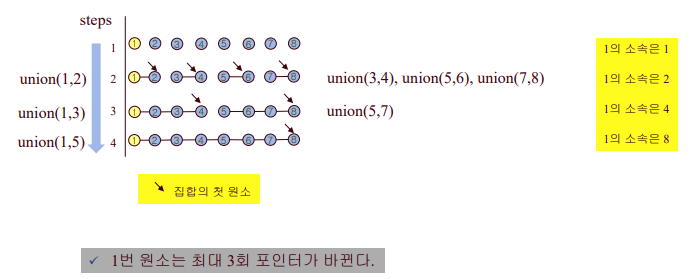
=> 한 원소에 대해 O(lg n)
=> 총 O(n lg n)
2) array 사용

set_id[i] : i가 속해있는 집합 이름
Operation
- find(x) : set_id[x] 반환
- union(x,y) : x에 속해있는 원소들을 y로 옮김 (set_id[x]를 set_id[y]로 바꿔줌)

linked list 때와 같은 방법으로 weighting-union heuristic 사용할 수 있고, (linked list 때와)같은 시간 소요됨
3) tree를 사용하는 방법
a) 단순한 방법
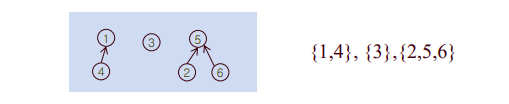
- 하나의 component(집합)는 하나의 트리로 표현
- 전체 그래프가 전체(모든) 집합을 나타냄
- root원소가 집합의 이름을 나타냄
- 각 원소는 parent로 향하는 포인터를 갖는다.
Operation
- find(x): x에서 출발하여 parent로 향하는 포인터를 따라 root로 이동하여, root값을 반환
- union(x,y): find(x) 원소를 find(y)의 child node로 만든다.


union(x1, xn) 수행시,

- 포인터 이동 횟수 : 1 + 2 + 3 + ... + (n-2) = (n-2)(n-1)/2 (한 노드씩 타고 올라가서 루트까지 감)
- 포인터 조작 횟수 : 1
-> O(n²) 시간 필요
b) 트리의 무게를 고려한 방법
개선점!
✓ 트리가 갖고 있는 원소의 수(weight)를 저장한다.
✓ 트리의 weight가 작은 것을 weight가 큰 트리에 연결한다.
~~ > find를 더 빨리 수행할 수 있게 된다. (결과 트리 높이가 낮은 것이 유리)
✓ 트리의 높이(height)를 이용하여 트리의 rank 정의. rank를 활용해도 같은 효과

n개의 원소가 있을 때, 이 방법으로 트리를 합치면 최종 트리 최대 높이는 lg n이다.
따라서 m회의 union, find 시간은 O(m lg n)이 된다.
c) path compression 방법

find(z) 수행시, 찾는 노드들을 root의 child로 만들어줌!
weighting-union heuristic + path compression
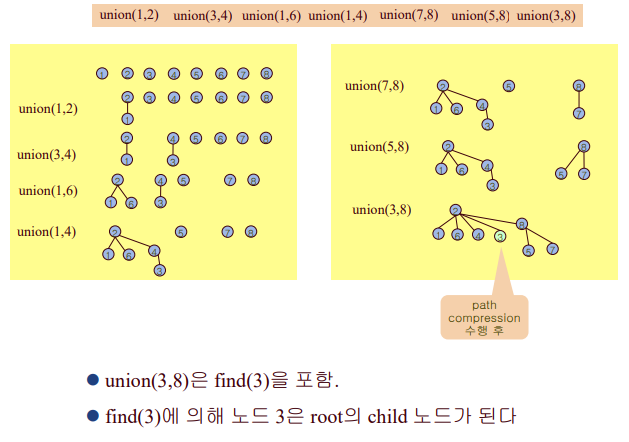
이때 시간복잡도는~?

G(100) = 4
union, find operation은 O(nG(n))을 가진다.
◆ Kruskal 알고리즘 분석 - tree, weighting union heuristic, path compression 사용
- 단위연산 : find, equal,merge 내에 있는 포인터 이동. 또는 데이터 비교문
- 입력크기 : 정점의 수 n과 엣지의 수 m
1. 에지들을 정렬하는데 걸리는 시간: Θ(m lg m)
2. n개의 disjoint set을 초기화하는데 걸리는 시간: Θ(n)
3. 반복문 안에서 걸리는 시간: 루프를 최대 m번 수행한다.
disjoint set data structure를 사용하여 구현하고, 1회 반복에서 find, equal, merge(union) 같은 동 작을 호출하는 횟수가 상수이면, m번 반복에 대한 시간복잡도는 Θ(m lg n) or (mG(m))이다
'CS > 알고릴라' 카테고리의 다른 글
| 6장. 분기 한정법(Branch-and-Bound) (0) | 2023.05.18 |
|---|---|
| 5장. 되추적 (Back-tracking) (0) | 2023.05.16 |
| 4장. 탐욕적인 접근방법 (Greedy Algorithm) (1) (0) | 2023.04.17 |
| 3장. 동적 계획법 (Dynamic Programming) (1) | 2023.04.13 |
| 2장. 분할 정복법 (Divide & Conquer) (0) | 2023.04.11 |




