센로그
3장. 동적 계획법 (Dynamic Programming) 본문
◆ 동적 계획법 (Dynamic Programming)
입력 크기가 작은 부분의 문제들을 해결한 후, 해당 부분 문제의 해를 활용해서 보다 큰 문제를 해결해나가는 알고리즘.
다음 두 가지 조건을 만족해야 동적 계획법으로 쓸 수 있다.
- 작은 문제들의 해를 활용해 큰 문제를 풀 수 있어야 함.
- 최적의 원칙 : 전체가 최적이면 부분에 대해서도 최적이어야 함.
◆ 분할 정복법 vs 동적 계획법
ㆍ분할 정복법
- 하향식(top-down) 해결법
- 큰 문제를 해결하는 데에만 관심이 있음
ㆍ동적 계획법
- 상향식(bottom-up) 해결법
- 작은 문제의 해결을 활용해 큰 문제를 해결
◆ 이항 계수(binomial coefficient) 구하기
분할 정복법 vs 동적 계획법으로 이항 계수를 구하는 법을 알아볼 것이다.
<이항계수 공식>

◆ 이항 계수 구하기 - 분할 정복법
bin(n-1,k-1) + bin(n-1,k) 을 재귀 호출해서 구함
계산량이 많은 n!이나 k! 대신 다음 식을 활용함

◇ 이항 계수 구하기 - 분할 정복법 코드
재귀적으로 계산
[pseudo code]
int bin(int n, int k) {
if (k == 0 || n == k) //아무것도 선택 안하는 경우, 전체 다 선택하는 경우는 하나
return 1;
else
return bin(n-1,k-1) + bin(n-1,k)
}
재귀를 사용하는 분할 정복식 접근 방법은
사람이 봤을때 간단하긴 하지만
내부적으로 동일한 문제를 중복해서 수행하게 되는 문제가 있다.

여기서 초록색을 두번 계산하게 됨!
nCk를 구하기 위해 이 알고리즘이 계산하는 항의 개수는 2*nCk -1이 된다. 넘많음!! ㅠㅠ
◆ 이항 계수 구하기 - 동적 계획법
Pascal의 삼각형 원리로 배열에 채워넣으며 구함


2차원 배열 B[i][j]에다 iCj값을 계산해 넣음
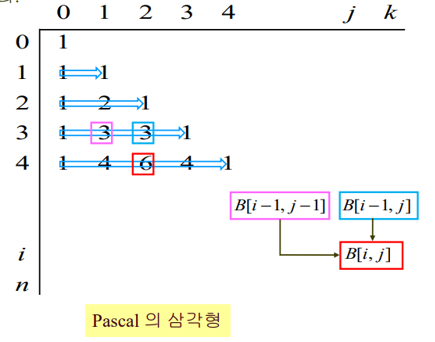
찾는 B[i][j]가 나올 때까지 왼쪽 위에서부터 배열을 하나씩 채워감
◇ 이항 계수 구하기 - 동적 계획법 코드
배열을 채워나가며 계산
[pseudo code]
int bin2(int n, int k) {
index i, j;
int B[0..n][0..k];
for(i=0; i <= n; i++)
for(j=0; j <= minimum(i,k); j++) //i와 k중 더 작은 값까지만 계산해줌
if (j==0 || j == i)
B[i][j] = 1;
else B[i][j] = B[i-1][j-1] + B[i-1][j];
return B[n][k];
}
j의 경우, i와 k 중 더 작은 값까지만 반복해주면 된다
왜냐하면 아무리 i가 크더라도 결국 nCk를 구할거면, k 뒤쪽으로는 계산 필요 없기 때문
(B[n][k]를 구하기 위해 최대 B[n-1][k]까지만 구하면 되므로 뒤엔 필요없음)
아래 그림 참고!
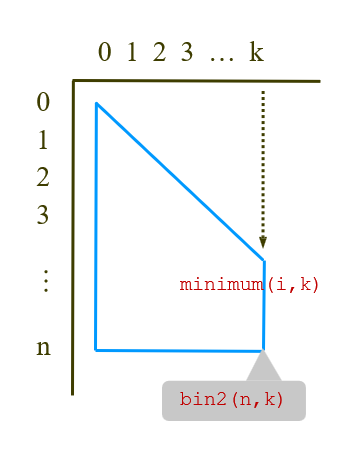
파란 면적이 계산 해야되는 부분임
◇ 이항 계수 구하기 - 동적 계획법 시간복잡도 분석
- 단위연산: for-j 루프 안의 문장
- 입력크기: n, k
i가 k 이상일 때는 j루프 수행횟수가 항상 k+1번이다.

따라서 총 수행횟수는,
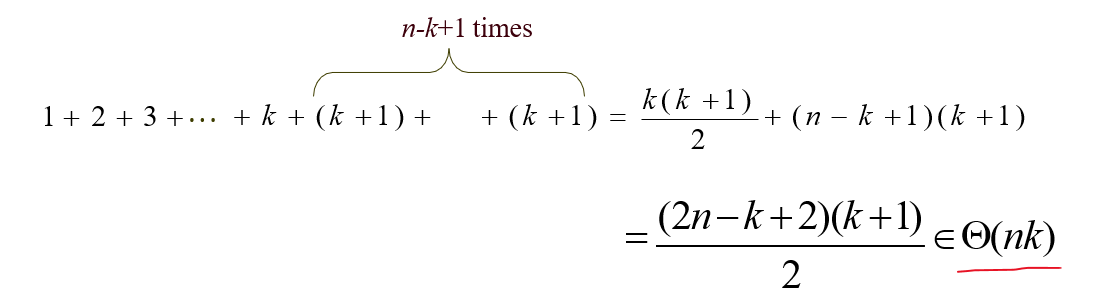
이므로 시간복잡도는 Θ(nk) 이다. (k ≤ n 이므로 k²항 대신 nk항만 보면 됨) <-??
◆ 최단 경로 문제 (all-pairs shortest paths problem)
그래프에서, 정점 vi에서 정점 vj로 가는 최단 경로를 찾는 방법에 대한 문제.
우리가 다룰 문제는 가중치가 포함된 그래프에서의 최단 경로 문제이다.
최단 경로문제는 최적화 문제에 속함!
※ 최적화 문제란? 주어진 문제에 대하여 하나 이상의 많은 해답이 존재할 때, 이 가운데에서 가장 최적인 해답(optimal solution)을 찾아야 하는 문제를 최적화문제(optimization problem)라고 한다.
|
◆ 최단 경로 문제 - 무작정 알고리즘
vi에서 vj로 갈 수 있는 모든 경로의 길이를 구하고 그중 최소 길이를 찾으면 됨.
그치만 너무너무 비효율적임!!
총 n개의 vertex가 있고, 모든 vertex들 사이에 edge가 존재한다고 가정했을 때,
vi~vj까지 가는 모든 경로의 개수는 (n-2)!이 될 것이기 때문. 굉장히 비효율적 ㅇㅇ
◆ 최단 경로 문제 - 동적 계획법
k까지 vertex를 활용한, i~j까지의 최단거리는
1) k-1까지 vertex를 활용했을 때의, i~j까지 최단거리
2) k까지 vertex를 활용해 만든, i~k까지의 최단거리 + k~j까지의 최단거리
이 둘중 하나이다!
D0를 가지고 Dn을 구할 수 있는 방법.

D0을 가지고 D1을 다 구하고, D1을 가지고 D2를 다 구하고... 이런 식!
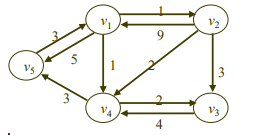

W: 가중치

D: 최단 경로의 길이

는 v1~ vk까지의 정점을 사용해서 만들 수 있는 최단 경로의 길이를 의미함.
(전부 다 사용할 필욘 없음! 가능한 것들 중에 젤 짧은거)
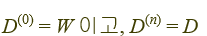
D0[i][j]는 vi~vj까지 아무 노드도 안 거치고 가는 경우이므로, vi~vj 사이의 가중치인 W
Dn[i][j]는 vi~vj까지 가는 경로 중 가장 짧은 경로(최종 해)를 의미하고, D라고 표기함
◇ 최단 경로 문제 - 동적 계획법
: Floyd의 알고리즘(1) 코드
D0부터 Dn까지, Dk-1의 정보를 활용해 Dk를 쭉 업데이트 해나가는 방법
void floyd(int n, const number W[][],number D[][]) {
int i, j, k;
D = W; // 가중치 배열로 초기화
for(k=1; k <= n; k++)
for(i=1; i <= n; i++)
for(j=1; j <= n; j++) // 행별로 실행
D[i][j] = minimum(D[i][j], D[i][k]+D[k][j]); // k-1번째의 D[i][j] 또는, k를 포험하는 D[i][j]
}
◇ 최단 경로 문제 - 동적 계획법
: Floyd의 알고리즘(1) 시간복잡도 분석
- 단위연산 : for-j 루프 안의 지정문
- 입력크기 : 그래프에서 정점의 수 n
모든 경우 시간 복잡도 T(n) = n*n*n = n³ 이다.
◇ Floyd의 알고리즘(1)에서 D를 하나만 써도 되는 이유
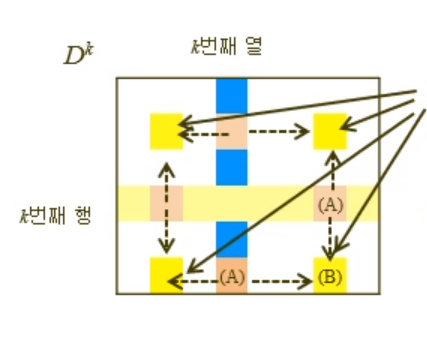
i행 j열 matrix D^(k)는 가로 방향(행별로)으로 업데이트를 하는데.
그렇게 되면 (B)보다 (A)를 먼저 업데이트 할 것이다.
근데!! (B) 업데이트시 필요한 k행, k열의 정보는 D^(k-1) 에서의 정보인데, (A)가 업데이트 되고나면 k행, k열은 D^(k)번째 정보가 된다 ㅠㅠ
그러면 안되능 거 아닌감?
--> ㅇㅇ 아님 괜찮음. k번째 업데이트에서, k번째 행과 k번째 열의 값은 k-1번째에서의 값에서 변동이 없기 때문임. 아래 수식 참고 ㄱㄱ
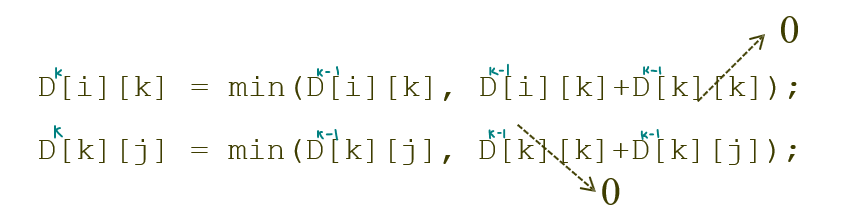
따라서 k의 버전마다 D를 따로 만들 필요 없이, 계속 덮어쓰면 된다! 라는 결론~
◇ 최단 경로 문제 - 동적 계획법 코드
: Floyd의 알고리즘(2)
경로의 정보까지 저장 (P[i][j])
[pseudo code]
void floyd2(int n,const number W[][],number D[][],index P[][]) {
index i, j, k;
for(i=1; i <= n; i++)
for(j=1; j <= n; j++)
P[i][j] = 0;
D = W;
for(k=1; k<= n; k++)
for(i=1; i <= n; i++)
for(j=1; j<=n; j++)
if (D[i][k] + D[k][j] < D[i][j]) { //중간에 k를 거치는 게 원래보다 더 짧다면
P[i][j] = k; //p[i][j]를 k값으로 업데이트
D[i][j] = D[i][k] + D[k][j]; //D[i][j]도 k를 거친 거리로 업데이트
}
}

최종적으로 P[i][j]에 저장된 값은, i~j까지 가는 최단 경로상에 있는 가장 순번이 큰 노드가 됨
1~n까지 k를 증가시키면서, 중간에 k를 거치는 게 원래보다 더 짧다면 k로 업데이트 하기 때문임

◇ Floyd의 알고리즘(2)에서 경로 출력하기
[pseudo code]
void path(index q,r) {
if (P[q][r] != 0) { //q~r로 바로 가지 않는 경우
path(q,P[q][r]); //q에서 P[q][r]로 가는 경로 호출
cout << “ v” << P[q][r];
path(P[q][r],r); //P[q][r]에서 r로 가는 경우 호출
}
}
◆ 연쇄 행렬곱셈
행렬을 연쇄적으로 곱할 때, 어느 순서로 곱하는 게 가장 곱셈 횟수를 줄일 수 있을까? 에 관한 문제.
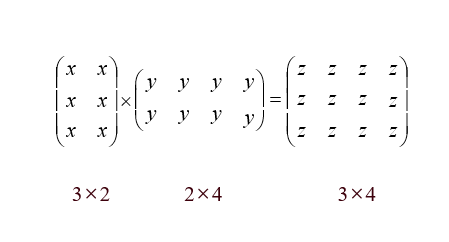
그림에서 행렬 곱셈을 위해 3 * 2 * 4회의 곱셈이 필요함!
A[i][k] x B[k][j]를 곱할때 필요한 곱셈 횟수는 총 i * k * j 회.
◆ 연쇄 행렬곱셈 - 무작정 알고리즘
가능한 순서를 모두 고려해보고, 그 중에서 가장 최소를 선택하는 방법.
행렬 A₁~An 까지 곱할 수 있는 모든 순서의 가짓수를 tn이라 하자.
이때 다음 부등식이 성립함.
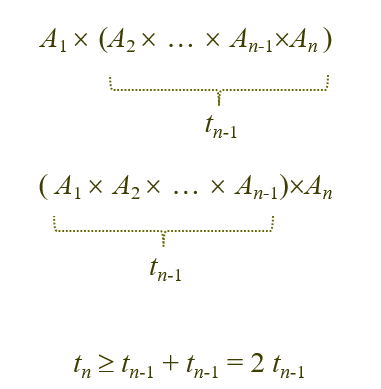
이렇게 쭉 t₂ 까지 가보면, ( t₂ = 1임)
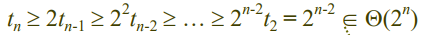
시간 복잡도가 최소한 지수 시간(2ⁿ)만큼 걸린다는 걸 알 수있음.
굉장히 비효율적이죠?
※ n개의 행렬을 곱하는 경우, 총 몇가지 순서로 곱할 수 있을까?
무작정 알고리즘의 모든 가능한 가지 수를 P(n)이라 할 때,

ex) 2개의 행렬을 곱하는 경우 다음 식과 같이 1가지의 순서로 곱할 수 있다.(t₂ = 1)
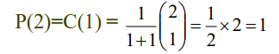
◆ 연쇄 행렬곱셈 - 동적 계획법
M[i][j]의 최솟값을 찾기 위해, i<=k<=j-1인 k를 기준으로 나눈 두 행렬끼리 곱하는 걸로 함. 인접행렬 수가 적은 것부터 시작해서, 점점 곱하는 행렬의 개수를 늘려감. 나눈 두 행렬 안에서의 곱셈은 이미 최소 횟수를 찾아놓은 상태일 것. 곱하는 행렬의 개수가 하나 늘어날 때마다 k값을 i부터 j-1까지 조절해서, 그 두 행렬을 곱할 때 최소 곱셈 횟수를 구한다.
M[i][j] 라는 배열을 도입한다.
이 배열은 i ≤ j 일 때, Ai부터 Aj까지의 행렬을 곱하는데 필요한 곱셈의 최소 횟수를 나타내는 배열이다.
M[i][j]는 다음과 같은 방식으로 업데이트 한다.
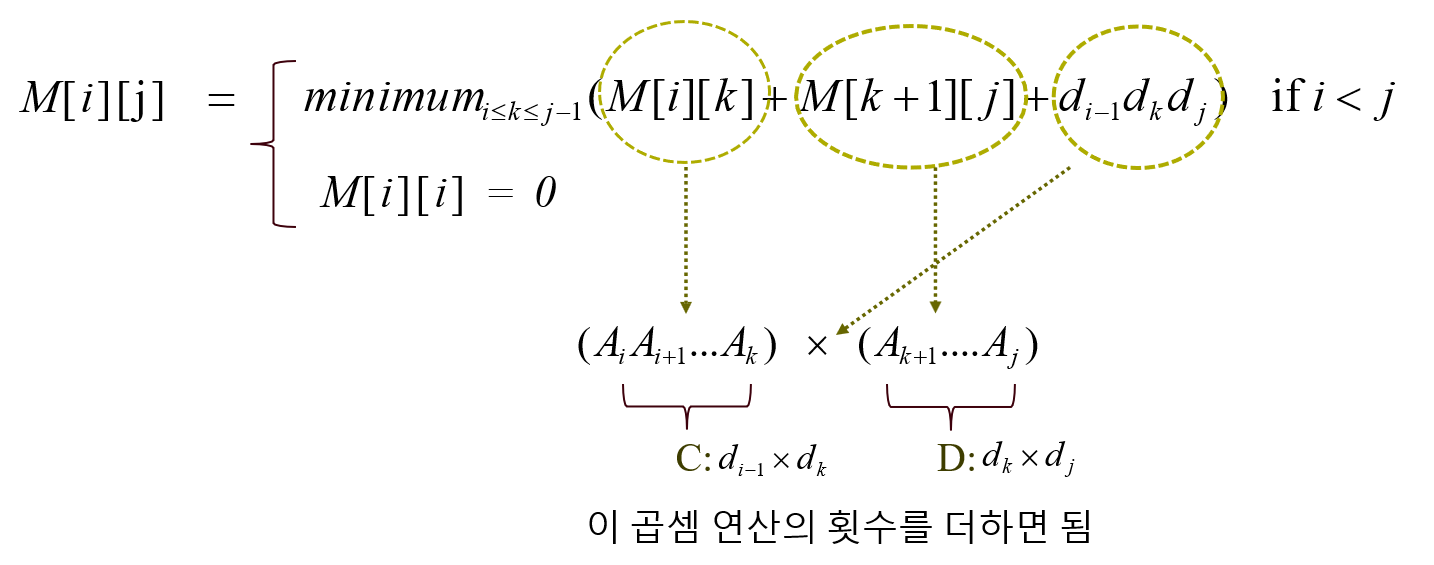
k를 i에서부터 j-1까지 움직이면서, Ak에서 갈라서 곱하면 곱셈 횟수가 최소가 된다! 싶으면
그 시점에서의 총 곱셈 횟수로 M[i][j]를 업데이트 함.
이때 총 곱셈 횟수는 M[i][k] + M[k+1][j] + (di-1 * dk * dj)

그런 식으로 M[i][j]를 채워나가면서 문제를 풂!
이때, 최적 순서까지 알기 위해, Floyd2 에서 했던 것처럼 별도의 행렬(P[i][j])을 하나 더 도입함.
M[i][j]를 업데이트 할 때, 그 시점의 k값을 P[i][j]에 기록함.

◇ 연쇄 행렬곱셈 - 동적 계획법 코드
diagonal 순으로 진행하며, k값을 조절해 M[i][j]의 최솟값(최소 횟수)을 채택해나가며 최종적으로 M[1][n]을 구하는 방법
[pseudo code]
int minmult(int n, const int d[], index P[][]) { // n은 행렬의 개수. d[i-1][i]는 i번째 행렬의 규모
index i, j, k, diagonal;
int M[1..n][1..n];
for(i=1; i <= n; i++)
M[i][i] = 0; // diagonal 0을 모두 0으로 초기화
for(diagonal = 1; diagonal <= n-1; diagonal++) // diagonal은 n-1까지 있을것
for(i=1; i <= n-diagonal; i++) {
j = i + diagonal;
i <= k <= j-1인 k에 대하여,
M[i][j] = minimum(M[i][k]+M[k+1][j]+d[i-1]*d[k]*d[j]);
P[i][j] = 최소치를 주는 k의 값
}
return M[1][n]; // 1부터 n까지 다 곱할때의 최소 횟수
}

전 단계 diagonal들에서 이미 계산된 값들(그 자리 기준 왼쪽 값들, 아래 값들 이용)을 이용해서 다음 diagonal 계산함
Diagonal 1부터 진행하는것의 의미는, 인접한 행렬의 개수가 적은 것들의 문제를 풀어서 점점 인접한 행렬의 개수가 많은 쪽의 계산으로 나아가는 것을 의미함
■ 최적 이진트리 순서까지 출력하려면?

order 함수의 시간복잡도 T(n) ∈ Θ(n)
◇ 연쇄 행렬곱셈 - 동적 계획법 시간복잡도 분석
- 단위연산: 각 k값에 대해 실행된 명령문
- 입력크기: 곱할 행렬의 개수 n

따라서, Θ(n³) 에 속한다.
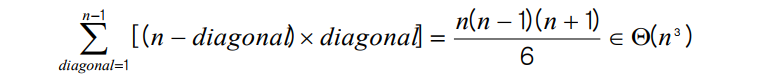
◆ 최적 이진검색 트리 (Optimal binary search tree)
데이터를 트리에 저장할 때, 그 데이터를 찾게될 확률(빈도)를 알고 있다면
자주 찾는 데이터를 루트에 가깝게 위치하도록 하는 방법. (데이터를 찾는 데 걸리는 평균 시간이 최소가 되도록)
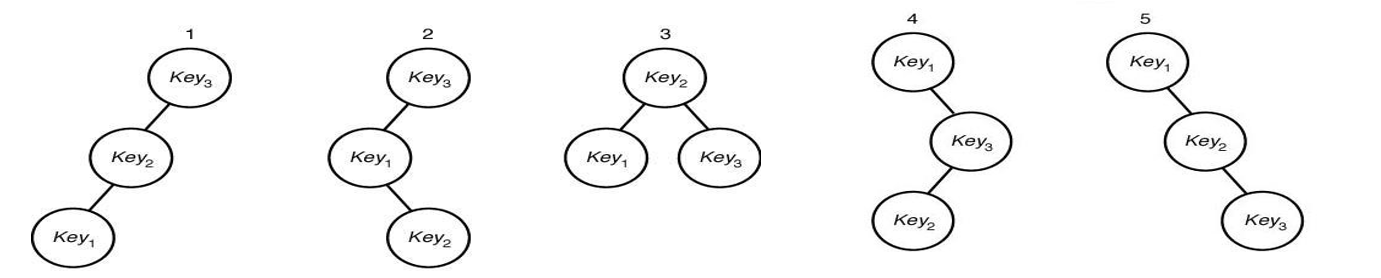
p_i 를 Key_i가 검색키일 확률이라 하고,
c_i 를 Key_i를 찾는 데 필요한 비교 횟수라 할때,
위 모양의 이진 트리들 각각에서의 평균 검색 시간(횟수)은 다음과 같이 표현할 수 있다.

당연하지만, 자주 찾는 걸 위에 올려놓은 5번이 제일 짧은 시간이 걸림!!
Key_i부터 Key_j까지 키를 포함하는 최적 이진검색 트리는, 평균 검색시간

를 최소화해야 함!
키가 세 개인 경우는 모든 경우를 생성해보고 최적이 뭔지 찾을 수 있지만, 키의 개수가 많아질수록 계산량이 늘어난다.
n개의 노드를 가진 이진 검색 트리 구성할 때 가능한 경우의 수는 아래와 같이 Catalan number로 표현할 수 있다.
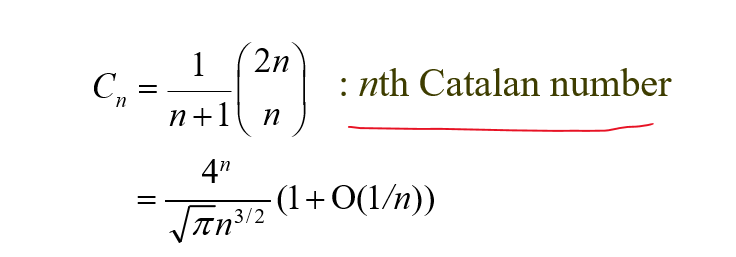
키의 개수가 많아질수록 굉장히 비효율적인 계산이 나오겠지?
그러니까 동적 계획법을 사용해서 좀 더 효과적인 방법으로 최적 이진 트리를 찾아보자!
◇ 최적 이진검색 트리 - 동적 계획법
diagonal 순으로 진행하며, k값을 조절해 최솟값(평균 검색시간의 최소)을 채택해 나가며 최종적으로 A[1][n]을 구하는 방법
<특징>
A[1][n]이라는 가장 큰 문제를 해결하기 위해서 작은 문제 A[i][j]들을 풀어나간다.
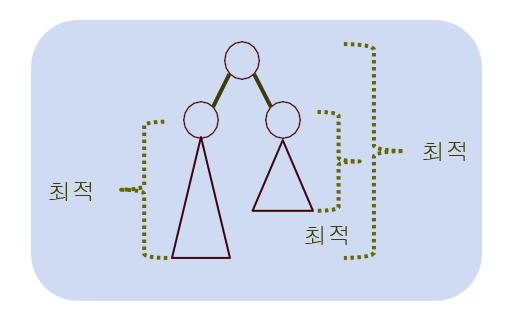
또, 생성된 최적 이진검색 트리는 최적의 원칙을 만족한다.
<사용 개념>
n개의 키가 있을 때, k번째 키를 루트로 하는 트리를 트리 k 라고 한다.
Key_i부터 Key_j를 포함하는 이진 검색트리의 평균 검색시간의 최솟값을 A[i][j]에 저장한다고 하자.
총 검색시간은 A[1][n]이라 할 수 있다.
A[i][j]가 업데이트 될 때, R[i][j]에는 그 시점에서 루트에 해당되는 키 값으로 업데이트 해준다.
<목표>
우리는 이 배열 A를 채우는 걸 목표로 함! k가 루트일 때, 아래와 같이 재귀적으로 표현할 수 있음.

A[1][n]은 왼쪽 서브트리에서의 평균 시간 + 오른쪽 서브트리에서의 평균 시간 + 루트에서 비교하는 시간(모든 노드를 처음에는 루트에서 비교하므로) 으로 나타낼 수 있다.
이 식을 A[i][j]에 대해 일반화하면 다음과 같다.
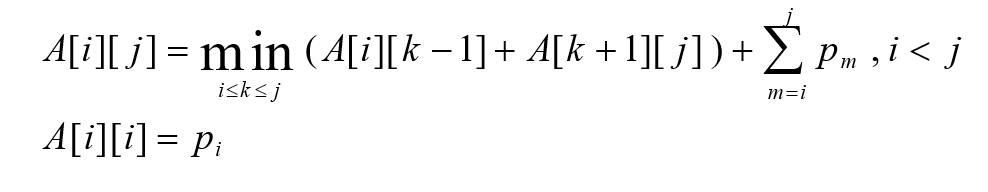
이걸 가지고 2차원 배열 A를 채워나가서, 최종적으로 A[1][n]의 값을 얻으면,
그것이 최적 이진검색 트리의 평균 검색시간(최적값)이 될 것이다.
[pseudo code]
void optsearchtree(int n, const float p[], float& minavg, index R[][]){
index i, j, k, diagonal;
float A[1..n+1][0..n];
for( i=1; i<=n; i++){
A[i][i-1]=0; A[i][i]=p[i]; R[i][i]=i; R[i][i-1]=0;
}
A[n+1][n]=0;
R[n+1][n]=0;
for(diagonal=1; diagonal<=n-1; diagonal++){
for(i=1; i<=n-diagonal; i++){
j = i+diagonal;
i <= k <= j인 k에 대해,
A[i][j] = min(A[i][k-1]+A[k+1][j])+ p_i~p_j까지의 합;
R[i][j] = 최소값을 주는 k의 값
}
}
}
minavg = A[1][n];
}
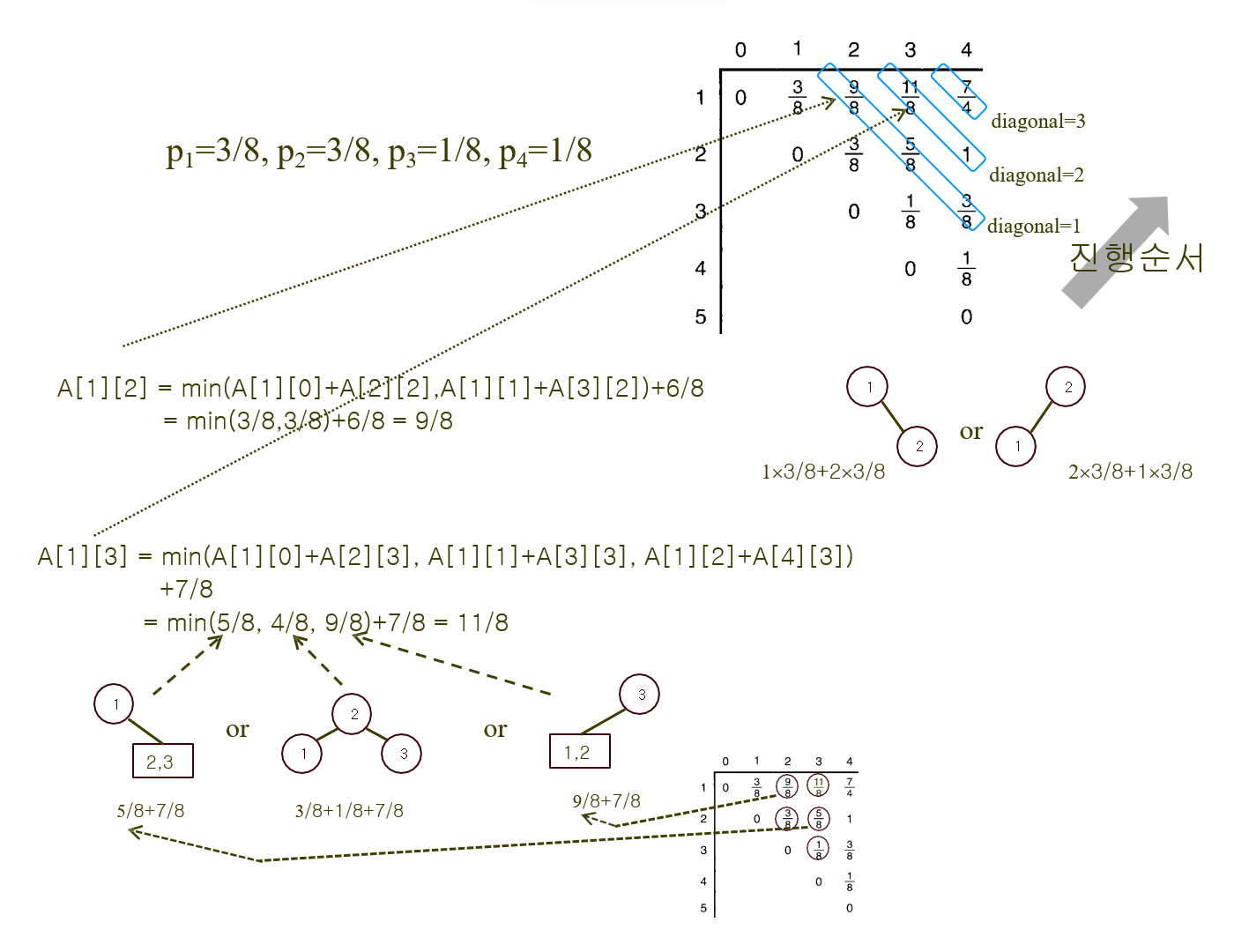
이렇게 구한 최적 이진 트리는 다음과 같이 출력하면 된다.
#include <iostream>
using namespace std;
void buildOptimalBST(int i, int j, const int R[][N], int parent, bool isLeft) {
if (i > j) return;
int root = R[i][j];
if (parent == -1)
cout << "Root: " << root << endl;
else
cout << (isLeft ? "Left child of " : "Right child of ") << parent << ": " << root << endl;
// 재귀적으로 왼쪽과 오른쪽 서브트리 구성
buildOptimalBST(i, root - 1, R, root, true); // 왼쪽 서브트리
buildOptimalBST(root + 1, j, R, root, false); // 오른쪽 서브트리
}
int main(){
buildOptimalBST(1, n, R, -1, true);
return 0;
}
■ 최소 곱셈 순서까지 출력하려면?

◇ 최적 이진검색 트리 - 동적 계획법 시간복잡도 분석
- 단위연산: 각 k값에 대해 실행된 명령문
- 입력크기: 키의 개수 n
행렬의 최소 곱셈 복잡도 분석과 유사하다.

따라서, Θ(n³) 에 속한다.
◆ DNA 서열 맞춤 (sequence alignment)
데이터들의 alignment를 어떻게 맞추는 게 가장 합당하냐? 에 관한 이야기.
DNA 서열 맞춤의 목적: 두개 유전자 비교해서, 사람은 쥐에 가깝나 코끼리에 가깝나 계산.
결과적으로, 사람은 쥐에 가깝다~ 또는 코끼리에 가깝다~ 하는 결론을 낼 수 있다.
다음과 같은 동족 서열이 있다 하자.

이 둘을 어떻게 맞추는 게 더 정확한지 판단하고자 한다.
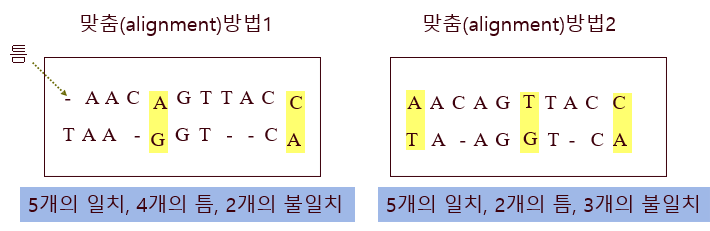
(틈이란 위치에 제거가 일어났거나, 상대편 서열에 삽입이 일어났다는 것을 의미함. 때문에 비워놓는게 더 잘맞는 ㅇㅇ)
이때 틈과 불일치의 손해를 정의해주면, 어떤 방법이 더 맞는 방법인지 판단할 수 있음.
◆ DNA 서열 맞춤 문제
우선 서열을 아래와 같이 배열로 표현한다.
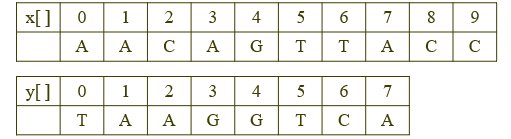
x[i]에서 끝까지, y[j]에서 끝까지의 두 배열을 맞추는 데 필요한 최소 비용을 opt(i,j) 라고 하자.
opt(0,0)은 우리가 구하려는 최종 비용이 될 것이다. (큰 문제)
(이때 opt(0,0)이 최적이면, opt(i,j)도 최적ㅇㅇ)
우리는 틈의 손해를 2, 불일치의 손해를 1이라고 가정하고 문제를 풀 것이다.
◆ DNA 서열 맞춤 문제 - 분할 정복법
시작 위치를 바꿔가며 이에 따른 틈 위치 결정. x,y중 하나를 끝까지 봤으면 재귀 종료하고 남은 칸에 틈 넣어주기.
<방법>
크기가 m인 서열 x와, 크기가 n인 서열 y를 입력받는다.
틈의 손해를 2, 불일치의 손해를 1이라 하자.
두 서열 중 어느 하나를 끝까지 비교한 경우까지, 아래 일반식을 재귀적으로 호출하며 두 서열을 비교한다.
일반식 : opt(i,j)=min(opt(i+1,j+1)+penalty, opt(i+1,j)+2, opt(i,j+1)+2)
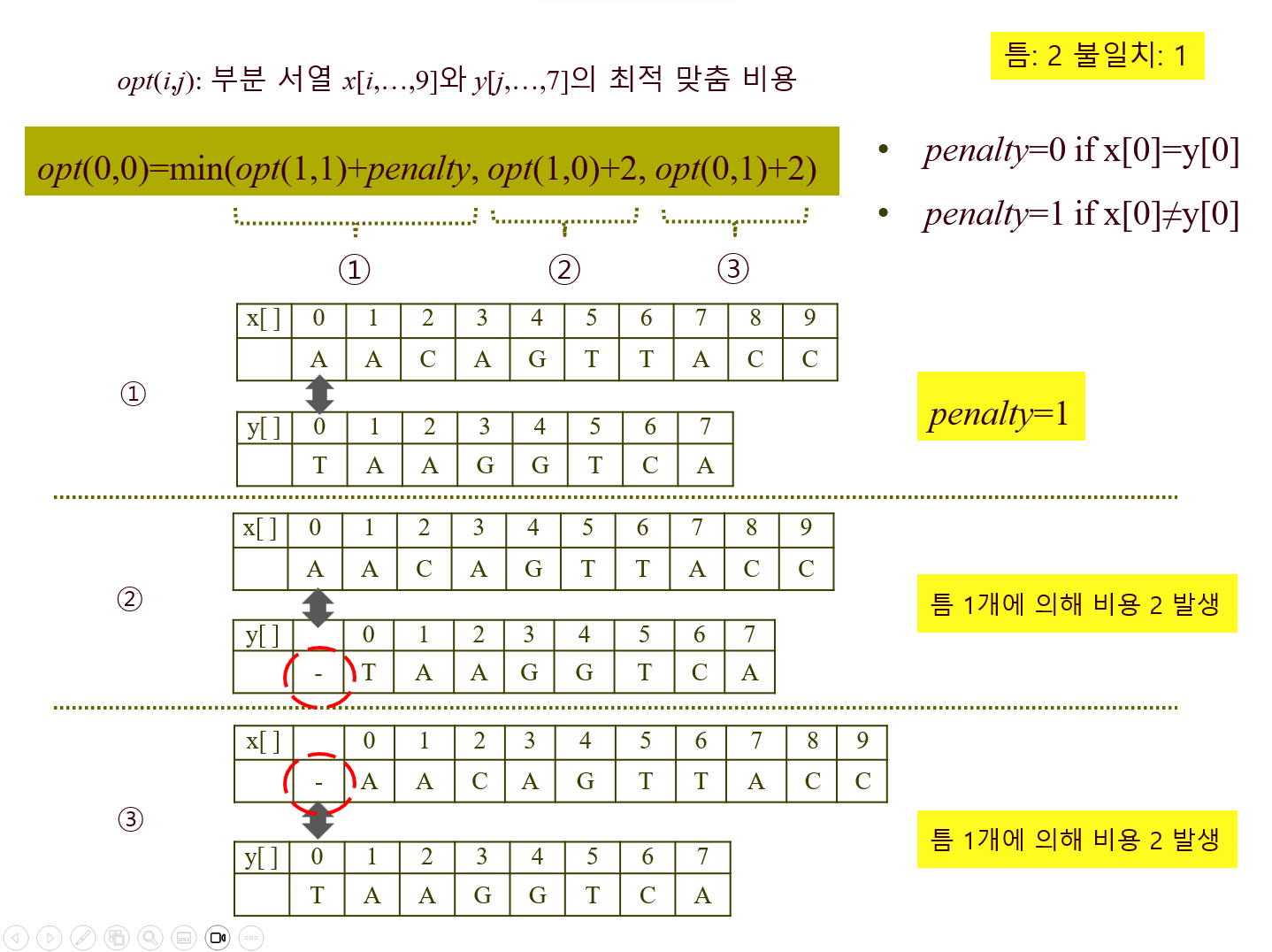
◇ DNA 서열 맞춤 문제 - 분할 정복법 코드
[pseudo code]
int opt(int i, int j) {
if(i==m) # x서열의 끝까지 갔으면,
opt_val = 2(n-j); # y서열의 남은 부분만큼 틈(비용 2)을 채워준다
else if(j==n) # y서열의 끝까지 갔으면,
opt_val = 2(m-i); # x서열의 남은 부분만큼 틈(비용 2)을 채워준다
else { # 둘다 아직 끝까지 안갔으면
if (x[i] == y[j]) # x와 y가 일치하면 패널티 없음
penalty = 0;
else # x와 y가 불일치(비용 1)하면 패널티 1
penalty = 1;
# 최소한 x,y 서열 중 어느 하나가 끝까지 갈 때까지 인덱스를 다르게 맞추며 재귀적으로 호출
opt_val = min(opt(i+1,j+1)+penalty, opt(i+1,j)+2, opt(i,j+1)+2)
}
return opt_val;
}optimal cost는 opt(0,0)의 반환값이 되겟죠?
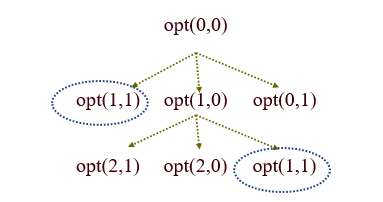
그렇지만, 분할 정복법을 이용한 서열 맞춤 방법은 비효율적이다.
이항계수 구하는 분할 정복법 알고리즘에서 처럼, 같은 함수를 중복해서 호출하기 때문임.
◆ DNA 서열 맞춤 문제 - 동적 계획법
2차원 배열을 활용해 푸는 방법
우선, 조건이 만족하는지 확인.
동적 계획법을 적용하기 위해서는 최적의 원칙이 적용되어야 함
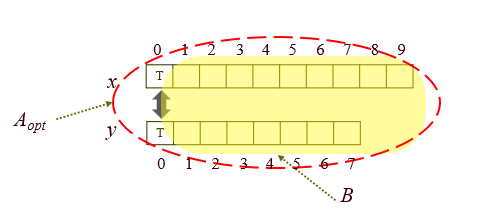
A_opt가 x[0~9]과 y[0~7]서열의 최적 맞춤이라 하자.
A_opt가 최적이면, A_opt에 속한 B도 x[1~9]와 y[1~7] 에 대해 최적이어야 한다.
이를 증명하기 위해, 우선 B를 최적이 아니라고 가정하자. 다시 말해, B보다 비용이 적은 맞춤 C가 존재한다고 하자.
그러면 A_opt에 B를 연결했을 때보다 C를 연결했을 때 비용이 더 작아질 것이다.
그러나 A_opt는 최적 맞춤이므로, 그런 C는 존재할 수 없다. 따라서 B도 최적임! ==> 최적의 원칙 성립
<방법>
1) 2차원 배열 채우기
주어진 배열들로부터 2차원 배열을 만들고, 마지막에 틈 행과 틈 열을 추가한다.
아래와 같이 틈 행과 틈 열의 손해를 채워넣는다. (끝 부분에 추가할 틈)
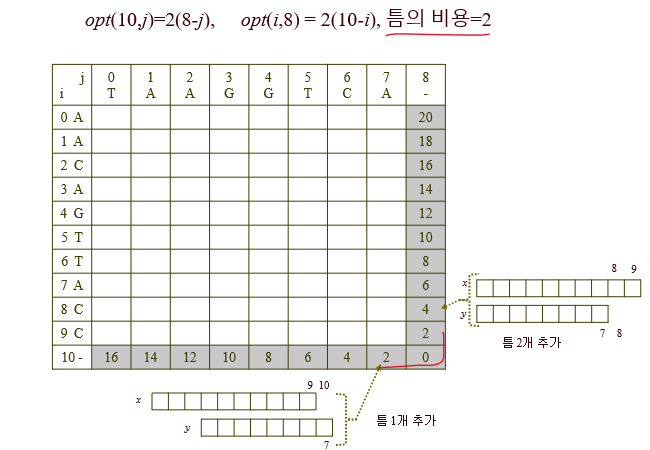
그런 다음, 우측 아래부터 대각 원소들을 채워나가며 작은 문제들부터 푼다.
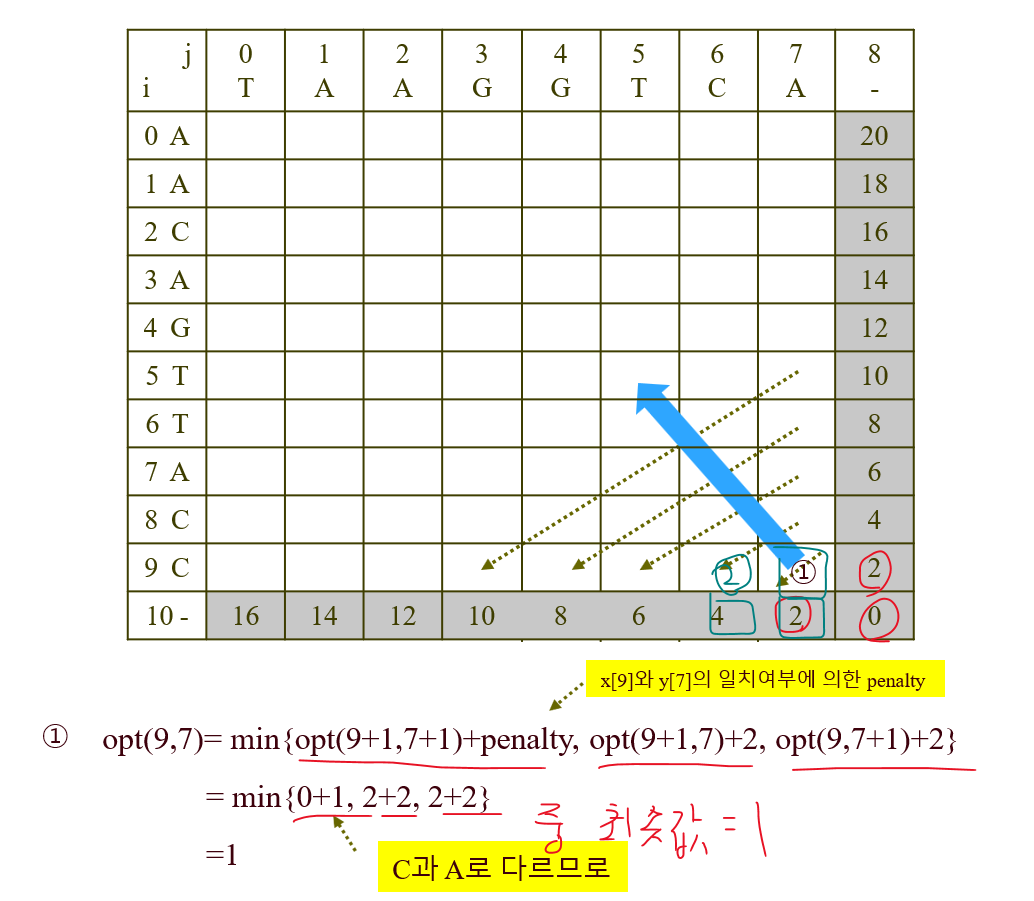
테이블의 최종 값▽
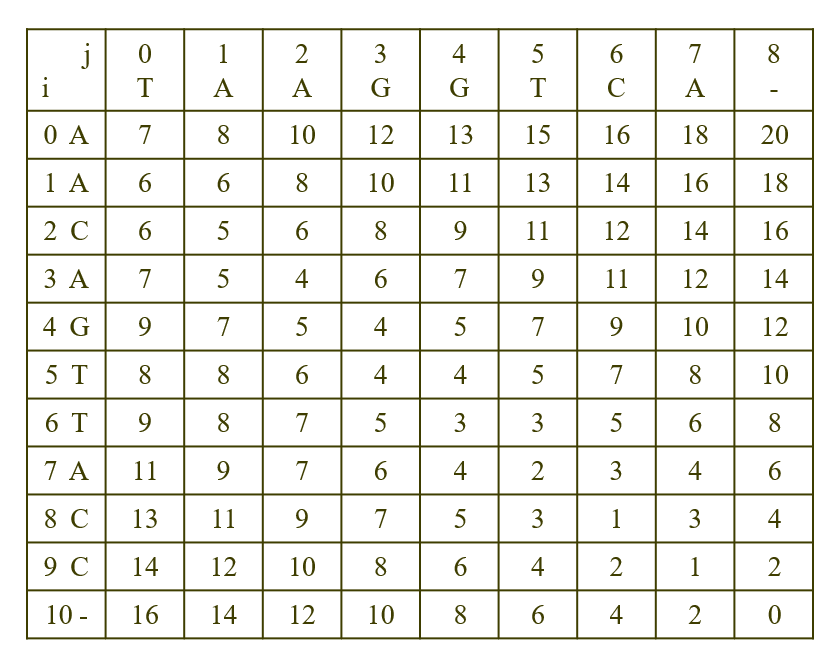
2) 2차원 배열을 바탕으로, 최적 서열 맞춤을 찾기
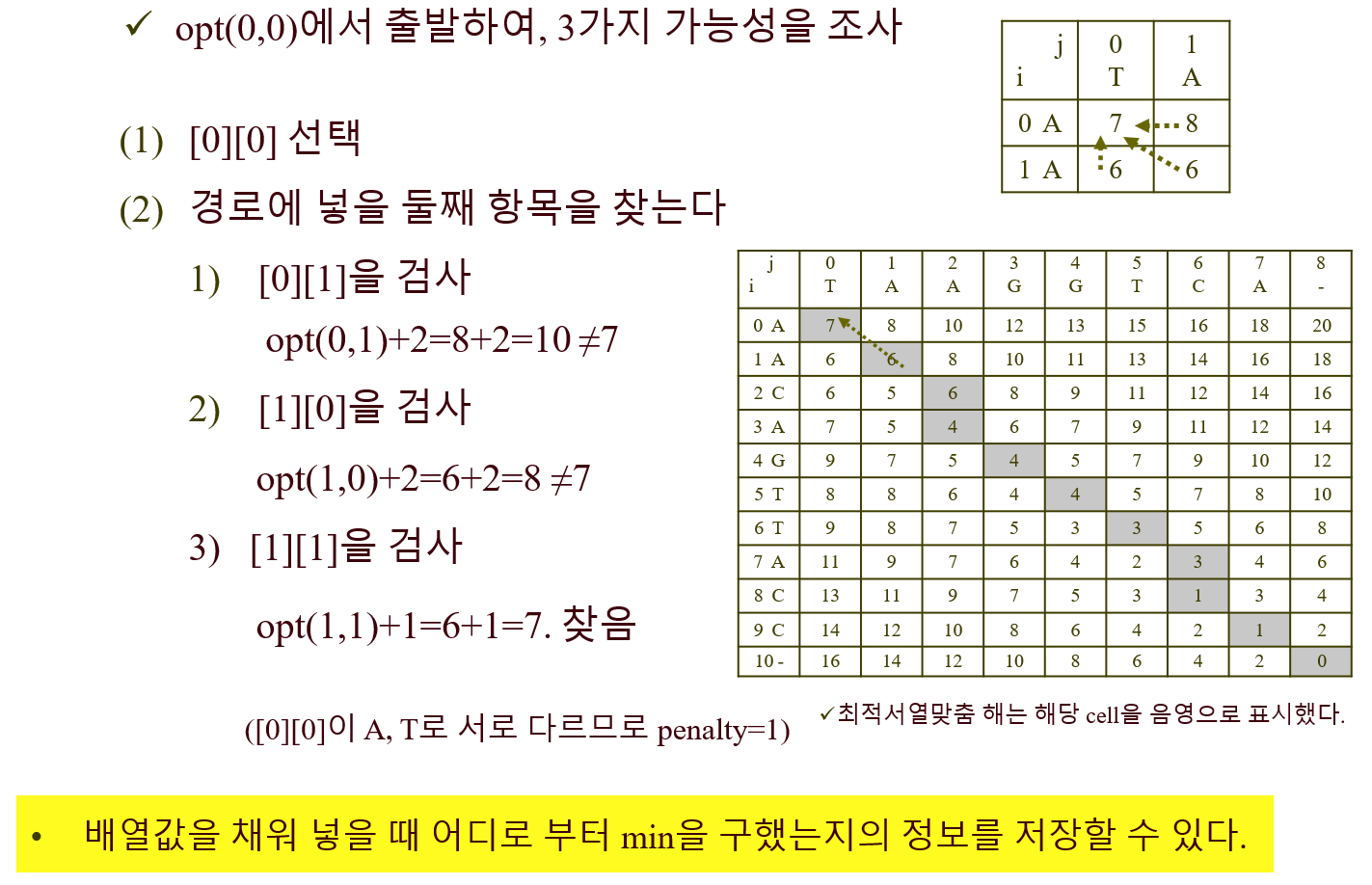
결과~
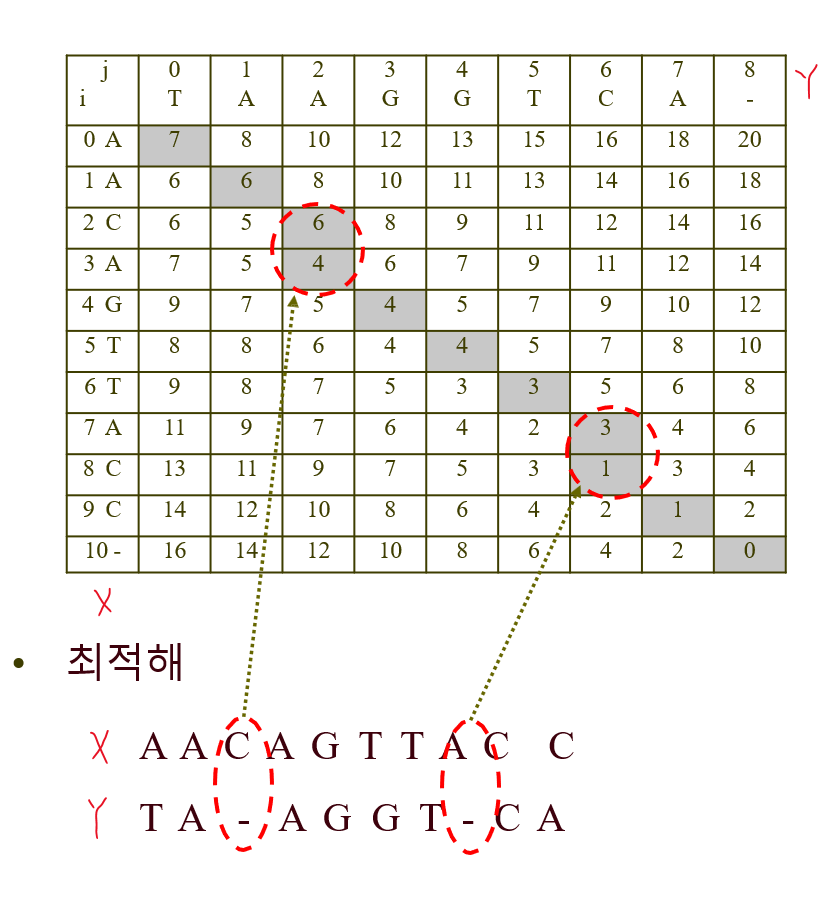
뒤에서부터 해를 채울 때,
대각선으로 가면 X,Y 둘다 값을 적고
위로 가면 Y에다 틈을 넣고
옆으로 가면 X에다 틈을 넣은 형태인 것이다.
◇ DNA 서열 맞춤 문제 - 동적 계획법 코드
[Python code]
a = ['A','A','C','A','G','T','T','A','C','C']
b = ['T','A','A','G','G','T','C','A']
m = len(a) # a의 크기
n = len(b) # b의 크기
table = [[0 for j in range(0,n+1)] for i in range(0,m+1)] # 틈 행과 틈 열 포함한 a,b의 2차원 배열
minindex = [[(0,0) for j in range(0,n+1)] for i in range(0,m+1)] # 어디에서 min값 구해온건지 저장
for j in range(n-1, -1, -1): # a[10] 틈행 초기화. n-1에서부터 -1전까지 -1칸씩
table[m][j] = table[m][j+1] + 2 # 틈의 손해인 2만큼씩 증가
for i in range(m-1, -1, -1): # b[8] 틈열 초기화. m-1에서부터 -1전까지 -1칸씩
table[i][n] = table[i+1][n] + 2 # 틈의 손해인 2만큼씩 증가
for i in range(m-1, -1, -1):
for j in range(n-1, -1, -1):
# 1번 방법 확인 (opt(i+1,j+1)+penalty)
penalty = 0
if (a[i] != b[j]):
penalty = 1
tmin = table[i+1][j+1] + penalty
minindex[i][j] = (i+1, j+1)
# 2번 방법 확인 (opt(i+1,j)+2)
if (timn > table[i+1][j] + 2):
tmin = table[i+1][j] + 2
minindex[i][j] = (i+1, j)
# 3번 방법 확인 (opt(i,j+1)+2)
if (tmin > table[i][j+1] + 2):
tmin = table[i][j+1] + 2
mininex[i][j] = (i, j+1)
table[i][j] = tmin
결과 출력 코드
x = 0
y = 0
while(x<m and y<n):
tx, ty = x,y
print(mininex[x][y])
(x,y) = minindex[x][y]
if x == tx+1 and y == ty+1:
print(a[tx], " ", b[ty])
elif x == tx and y == ty + 1:
print(" - "," ", b[ty])
else:
print(a[tx], " , " -")'CS > 알고릴라' 카테고리의 다른 글
| 5장. 되추적 (Back-tracking) (0) | 2023.05.16 |
|---|---|
| 4장. 탐욕적인 접근방법(Greedy Algorithm) (2) (0) | 2023.05.01 |
| 4장. 탐욕적인 접근방법 (Greedy Algorithm) (1) (0) | 2023.04.17 |
| 2장. 분할 정복법 (Divide & Conquer) (0) | 2023.04.11 |
| 1장. 알고리즘: 효율, 분석, 그리고 차수 (0) | 2023.03.06 |




