센로그
4장. 탐욕적인 접근방법 (Greedy Algorithm) (1) 본문
◆ 탐욕적인 알고리즘 (Greedy Algorithm) 이란?
현 단계(상태)에서 가장 좋다고 생각되는 답을 선택함으로써 최종적인 해답에 도달하는 방법.
현 시점의 가장 좋은 해는 local 최적해이다. 그러나 항상 이것들이 모여서 global 최적해를 만들진 않는다.
따라서, 탐욕적인 알고리즘을 사용하려면 항상 최적의 해답을 주는지를 반드시 검증해야 함!
◆ 탐욕적인 알고리즘 설계 절차
걍 이런게 있구나 알고, 실제 알고리즘에서 어떤 부분이 어느 단계에 속하는지 알면 됨
1. 선정 과정 (selection procedure)
현재 상태에서 가장 좋으리라고 생각되는(greedy) 해답을 찾아서 해답모음(solution set)에 포함시킨다.
2. 적정성 점검 (feasibility check)
새로 얻은 해답모음이 적절한지를 결정한다.
3. 해답 점검 (solution check)
새로 얻은 해답모음이 최적의 해인지를 결정한다.
◆ 탐욕적인 알고리즘 - 거스름돈 문제
동전의 개수가 최소가 되도록 거스름돈을 주는 문제.
<천원의 거스름돈을 가질수 있는 방법 중 가장 좋은 방법> (우리나라 ver)
: 천원짜리 한장을 챙긴다. (<- 다른 동전이나 지폐는 생각도 안하고, 천원짜리 하나만 가지고 생각하면 됨 ㅇㅇ 현 상태에서 가장 좋은 게 글로벌 최적해가 되므로, 이건 그리디 알고리즘 쓸 수 있음)
계산이 모두 끝나고 뒤로 돌아가서, '아 아까 1000원짜리가 아니라 500원짜리로 받앗어야해!' 라는 생각을 하진 않을 것.
따라서 다시 돌아갈 일도 없음.(돌아갈 일이 있다면 쓰면 안됨)
But..
동전 체계가 달라지면 local 최적해가 global 최적해가 안될 수도 있음.
12원짜리 동전을 새로 발행했다고 가정하자. 동전은 12원, 5원, 1원이 있음.
16원의 거스름돈을 줄 때, 그리디 알고리즘을 적용하면 다음과 같음

그러나 사실은 이거보다 동전을 적게 받을 수 있는 방법이 있었는데...▽

따라서 이건 그리디 알고리즘 쓸 수 없음!
◆ 그래프 (Graph) 용어 정리
G = (V,E)
G : 특정 그래프의 이름
V : vertex(노드) 의 집합
E : edge 의 집합
순서가 의미를 가지기 때문에 () 이 괄호를 쓴다.
◆ 신장 트리 (Spanning Tree)
모든 노드를 연결하는 순환경로(cycle)가 없는 그래프를 의미함.
(span : 밧줄로 매다)
ㆍ신장 트리(spanning tree)
모든 노드를 연결하는, 순환경로가 없는 그래프
ㆍ완전 그래프(complete graph)
모든 노드간에 엣지가 존재한다
노드가 n개인 완전 그래프 K_n의 엣지의 개수는 nC2
ㆍ t(G)
: graph 내에서, spanning tree의 개수
Cayley's formula
: G가 K_n인 경우, t(G) 는 최대 n^(n-2) 이다.
◆ 최소 비용 신장 트리 (Minimum Spanning Tree)
그래프에서 만들 수 있는 신장 트리 중에서, 최소의 비용이 되는 트리
여기서 최소의 가중치를 가진 부분 그래프는 반드시 트리가 되어야 함.
왜냐하면, 만약 트리가 아니라면, 분명히 순환경로(cycle)가 있을 것이고,
그렇게 되면 순환경로 상의 한 엣지(더 큰 비용이 드는)을 제거하면 더 작은 비용의 신장 트리가 될 수 있기 때문.
< MST 활용 예시>
| 도로건설 - 도시들을 모두 연결하면서 도로의 길이가 최소가 되도록 하는 문제 통신(telecommunications) - 전화선의 길이가 최소가 되도록 전화 케이블 망을 구성하는 문제 배관(plumbing) - 파이프의 총 길이가 최소가 되도록 연결하는 문제 |
◆ 최소 비용 신장 트리 - 무작정 알고리즘
모든 신장 트리를 다 고려해보고, 그 중에서 최소 비용이 드는 것을 고르는 방법
t(G) = 최대 n^(n-2)이므로 복잡도가 굉장히 나쁘다. ㅠㅠ
더 좋은 방법이 없을까? --> 그리디 알고리즘 ㄱㄱ
◆ 최소 비용 신장 트리 - 탐욕적인 알고리즘
1) G = (V,E)가 주어졌을 때, F⊆E인 G의 MST F를 정의함.
2) 시점마다 알고리즘에 따라 하나의 엣지를 선정하고, 이 엣지를 F에 추가해도 사이클이 생기지 않는다면 이를 F에 추가해가며 갱신
-> 뒤로 돌아오는 일 없이, 매 순간순간 최적의 해인지 판단하고 결정하는 탐욕적인 알고리즘의 일종임.
예시) Prim's 알고리즘, Kruskal 알고리즘 등
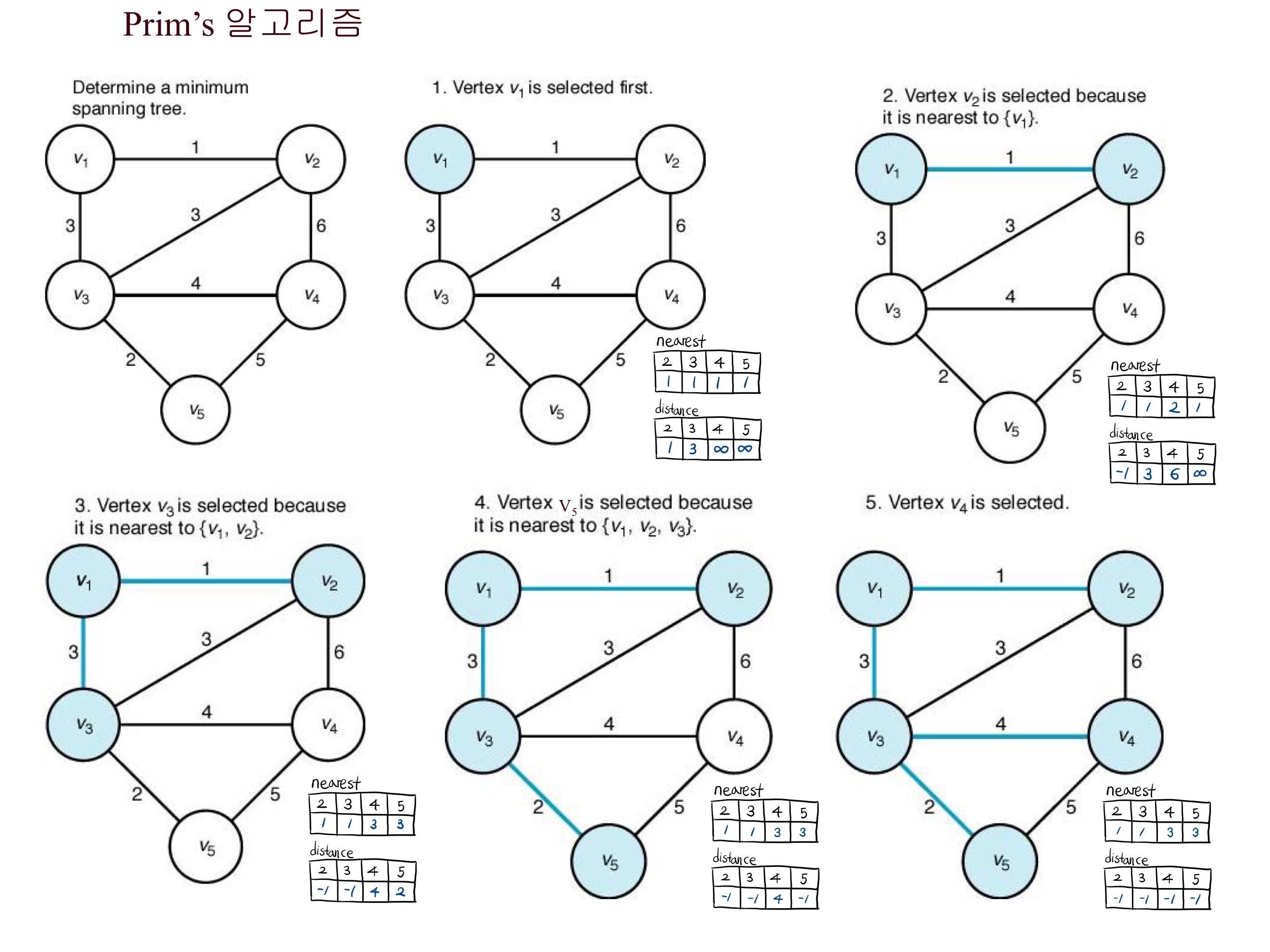
◆ Prim's 알고리즘
Y집합과 V-Y집합을 나눠서, 두 집합을 잇는 최소 가중치를 가진 엣지를 선택해 Y집합에다 추가해가며
최종적으로 Y트리(MST)를 만드는 방법.
< 방법 >
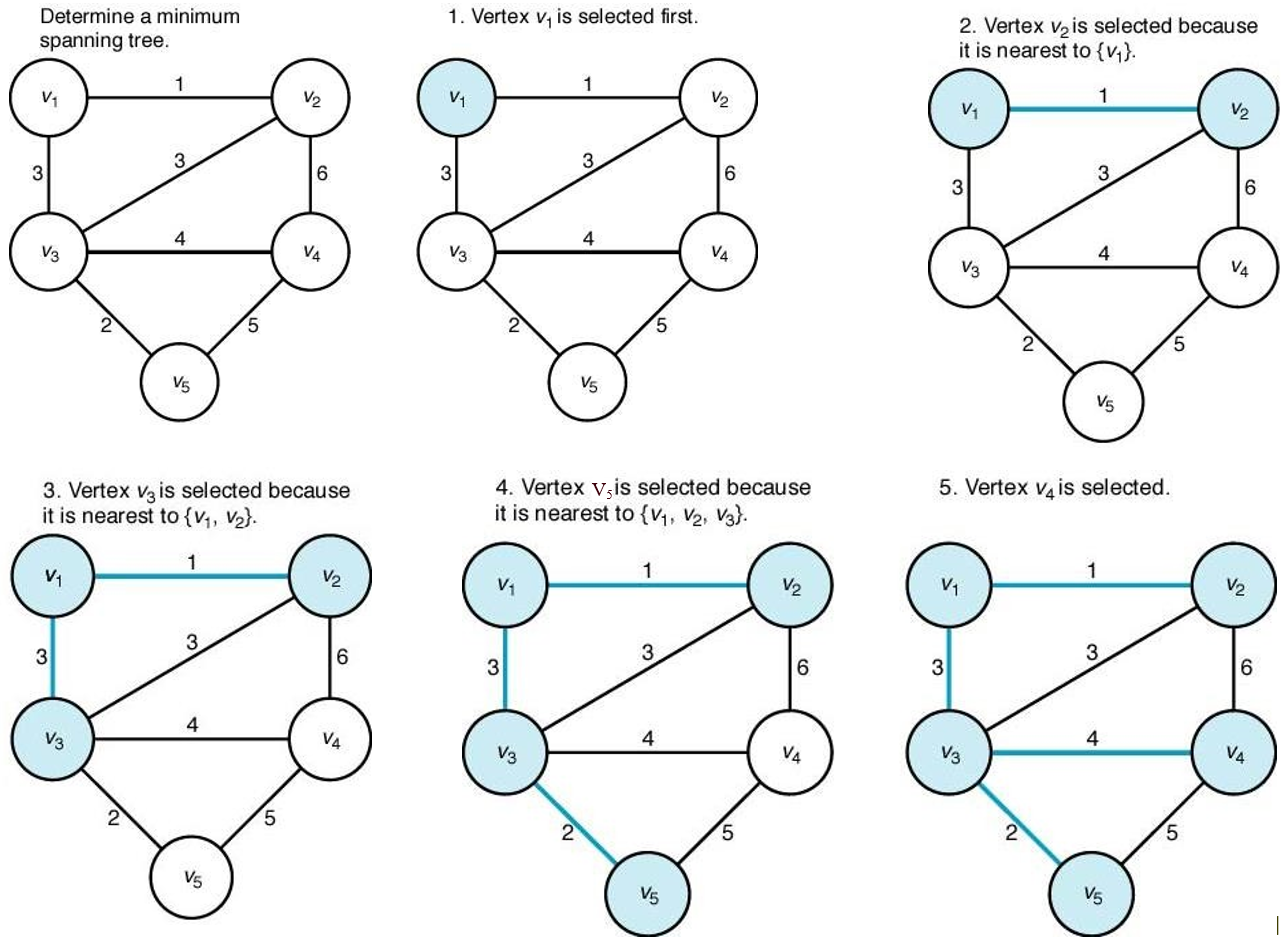
- 매 스텝에서 한번 파란색이 되면 번복안함. 그거로 끝!
- y집합과 v-y집합을 연결하는 엣지들 중에서는, 절대 트리 내에 사이클을 만들지 않음. <--각각 두 개의 독립된(서로소) 집단에서 가져왔기 때문임. 따라서 적정성 테스트 안해도 됨
< 사용 개념 >
ㆍW[i][j]

ㆍnearest[i]
Y에 속한 정점 중, vi와 가장 가까운 정점의 인덱스
ㆍdistance[i]
vi와, nearest[i]을 잇는 엣지의 가중치
◇ Prim's 알고리즘 - 코드
void prim(int n, const number W[][], // 입력: 정점의 수, 그래프의 인접행렬식 표현
set_of_edges& F) { // 출력: 그래프의 MST에 속한 엣지의 집합
index i, vnear;
number min;
edge e;
index nearest[2..n]; // Y에 속한 정점 중, vi와 가장 가까운 정점의 index
number distance[2..n]; // vi와 nearest[i]를 잇는 엣지의 가중치
// 초기화
F = Φ; // 최종 tree 일단 공집합으로 초기화
for(i=2; i <= n; i++) { // 첫 노드를 v1으로 잡고, nearest[]와 distance[] 초기화
nearest[i] = 1; // 처음엔 Y에 v1밖에 없으므로, 모든 노드에 대한 nearest[i] = 1로 초기화
distance[i] = W[1][i]; // 처음엔 Y에 v1밖에 없으므로, v1과 vi를 잇는 엣지의 가중치로 초기화
}
repeat(n-1 times) { // 처음 Y에 추가한 1을 제외하고 n-1번 반복
// Y에 속한 노드와 가장 가까운 V-Y의 노드인 vnear 찾기
min = ∞;
for(i=2; i <= n; i++) // 각 정점에 대해서
if (0 <= distance[i] < min) { // Y에 속한 노드와, V-Y에 속한 vi 사이의 가중치가 min보다 작은 경우
min = distance[i]; // min 업데이트(Y과 가장 가까운 V-Y의 노드 사이의 가중치)
vnear = i; // 그 노드의 index로 vnear을 업데이트
}
e = vnear와 nearest[vnear]를 잇는 엣지;
e를 F에 추가; // 새로 선정한 엣지를 반환할 MST에 추가
distance[vnear] = -1; // 찾은 노드를 Y에 추가한다.
// 업데이트된 Y와 V-Y 사이의 distance[i]가 감소할 수 있는지 확인
for(i=2; i <= n; i++)
if (W[i][vnear] < distance[i]) { // Y에 없는 각 노드에 대해서(Y에 있으면 무조건 > 방향 임)
// 새로 추가한 vnear과 V-Y의 노드의 거리가 기존 Y <-> V-Y의 거리보다 짧은 경우
distance[i] = W[i][vnear]; // distance[i]를 갱신한다.
nearest[i] = vnear; // nearest[i] 갱신
}
}
}distance[i] >= 0 이면 vi ∈ V-Y
distance[i] == -1 이면 vi ∈ Y
◇ Prim's 알고리즘 - 시간복잡도 분석
ㆍ단위연산 : repeat 루프 안에 있는 두 개의 for 루프 내부에 있는 명령문
ㆍ입력크기 : 정점의 개수, n
n에 대해서 루프가 2번이므로, T(n) = 2(n-1)(n-1) ∈ n² 이다.
◆ Kruskal 알고리즘
가중치가 작은 순서(비 내림차순)로 정렬해서, 이 순서대로 두 노드가 각각 속한 집합을 확인하고
서로 다른 집합이면(사이클을 만들지 않으면) 엣지를 연결한 것을 F에 추가하며 MST를 만들어감
< 방법 >
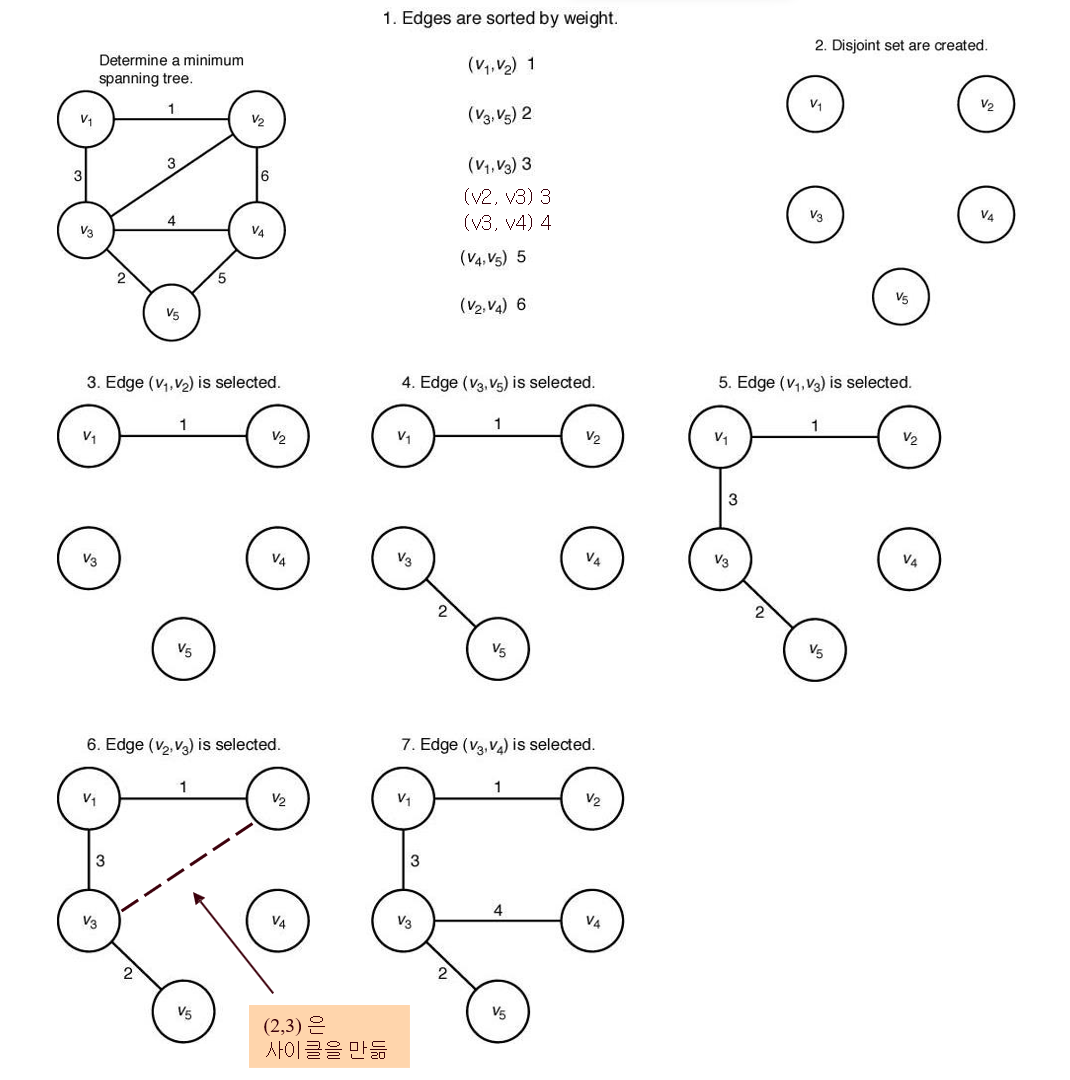
< 사용 개념 >
ㆍE[]
존재하는 엣지들의 집합. 이를 비내림차순으로 정렬한 후, 순서대로 꺼내서 확인하고 연결함
◇ Kruskal 알고리즘 - 코드
void kruskal(int n, int m, // 입력: 정점의 수 n, 엣지의 수 m
set_of_edges E, // 입력: 가중치를 포함한 엣지의 집합
set_of_edges& F) { // 출력: MST를 이루는 엣지의 집합
index i, j;
set_pointer p, q;
edge e;
F = ϕ;
E에 속한 m개의 엣지를 가중치의 비내림차순으로 정렬;
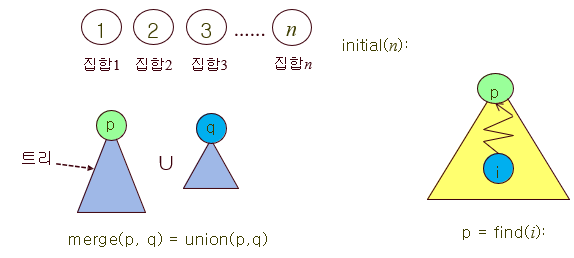
initial(n); // 노드들을 각각 서로소(서로 중복 원소 X) 집합으로 만듦. 총 n개의 집합이 만들어 질 것.
while (F에 속한 엣지의 개수가 n-1보다 작다) { // MST에 n-1개의 엣지가 들어가면 완성된 것
e = 아직 점검하지 않은 최소의 가중치를 가진 엣지;
(i, j) = e를 이루는 양쪽 정점의 인덱스;
p = find(i); // i노드가 포함된 트리의 루트의 이름을 리턴
q = find(j); // j노드가 포함된 트리의 루트의 이름을 리턴
if (!equal(p,q)) { // i가 속한 트리와 j가 속한 트리가 다른 경우
merge(p,q); // 두 트리를 합친다.
e를 F에 추가; // MST에 p,q 집합 사이의 엣지 정보를 추가.
}
}
}
◇ Kruskal 알고리즘 - 시간복잡도 분석
Ackermann's function
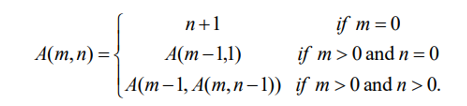
Ackermann 함수를 다음과 같이 단순화 시킨 함수를 F(n)이라 하자.
G(n)은 F(n)의 역함수로 정의함.
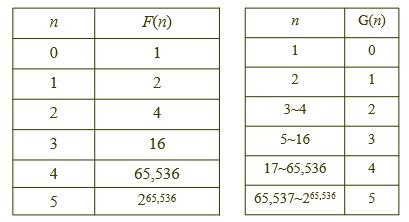
이때, merge연산과 find 연산은 최악의 경우 O(nG(n)) 만큼의 복잡도를 가진다.
-
ㆍ단위연산 : find(), equal(), merge() 내에 있는 포인터 이동 또는 데이터 비교문
ㆍ입력크기 : 정점의 개수 n, 엣지의 개수 m
1) 엣지들을 정렬하는 데 걸리는 시간은, 퀵소트 사용한다고 치면 Θ(m logm)
2) n개의 서로소 집합을 초기화하는 데 걸리는 시간은, Θ(n)
3) 반복문 안에서는 루프를 최대 m번 수행한다. Θ(m logn) or Θ(mG(m))
루프 안에서 최악의 경우는, 모든 정점이 서로 연결된 경우( m = n(n-1)/2 )이다.
이를 위의 결과에 대입하면, W(m,n) ∈ Θ(n² logn)
◆ Prim's 알고리즘 vs Kruskal 알고리즘

Sparse 그래프(엣지가 상대적으로 적은 그래프)인 경우, 엣지 단위로 판단하는 Kruskal 알고리즘이 더 효과적
Dense 그래프(엣지가 상대적으로 많은 그래프)인 경우, node 단위로 판단하는 Prim's 알고리즘이 더 효과적
'CS > 알고릴라' 카테고리의 다른 글
| 5장. 되추적 (Back-tracking) (0) | 2023.05.16 |
|---|---|
| 4장. 탐욕적인 접근방법(Greedy Algorithm) (2) (0) | 2023.05.01 |
| 3장. 동적 계획법 (Dynamic Programming) (1) | 2023.04.13 |
| 2장. 분할 정복법 (Divide & Conquer) (0) | 2023.04.11 |
| 1장. 알고리즘: 효율, 분석, 그리고 차수 (0) | 2023.03.06 |




