센로그
10. Euler transforms and quaternions 본문
◆ Euler Transform
euler angle을 사용해 변환하는 과정
※ 이거~


x,y,z축(주축)을 기준으로 회전 가능
=> 임의의 축으로 회전하려면, 주축으로 맞춰서 회전하고 다시 원래대로 돌려줬었다
근데 이러면 불편하기도 하고, 문제도 발생함

회전할 때의 order(순서)가 굉장히 중요하다! 순서가 바뀌면 결과가 완전히 달라짐
◆ Keyframe Animation in 2D
keyframe을 사용하여 제작하는 Animation
전통적으로 애니메이션 제작에서는, 시니어 아티스트가 키 프레임을 그리고 주니어 아티스트가 이 사이를 채우는 방식.
근데 이런 방식은 너무 비용이 많이 든다! => 컴퓨터가 자동으로 채워주는 알고리즘이 등장
keyframe들만 정의해주고, keyframe 사이의 frame들은 자동으로 보간되어 채워지도록 함.
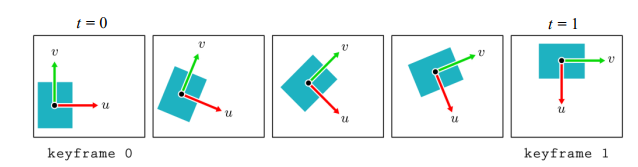
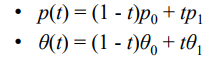
center position p와 orientation angle θ 자동으로 보간되어 채워지도록 함.
사이사이의 center position 및 orientation angle을 샘플링한다! 라고 함.
근데, 아래 그림을 보자
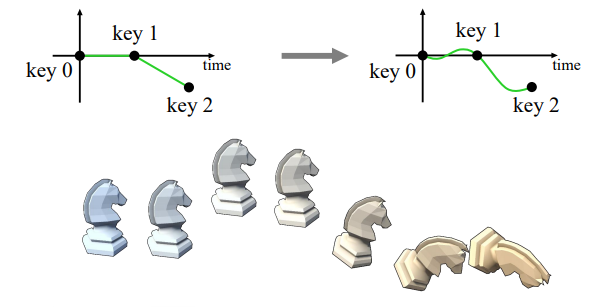
왼쪽처럼 각진 그래프의 경우 보간한 움직임이 부자연스러울 수 있음!
포물선운동은 ∧이렇게 안 생기고 ⌒이렇게 생겼자나 ㅇㅇ 그래서 각진 거 표현할 때 끊겨보일 수 있다.
이런 문제를 해결하기 위해서, smoothing algorithm을 쓸 수 있음.
1차원 선형보다는, 2차원, 3차원.. 의 high-order 그래프가 훨씬 부드러움. 이런걸 사용해서 보간함
◆ Euluer Transform - 문제점
이제 Euler Transform의 문제점을 보자.
Euler Transform은 굉장히 직관적이고 사용하기도 쉬워. 그러나.. 다음 두가지 문제점이 존재한다.
1) Rotation interpolation시 문제
두 개의 서로 다른 Euler rotation을 interpolation할 때 문제가 생김.
우선 화살표를 (x, y, z)축 기준으로 (60, 30, 45)만큼 회전시킨 상태라고 하자.
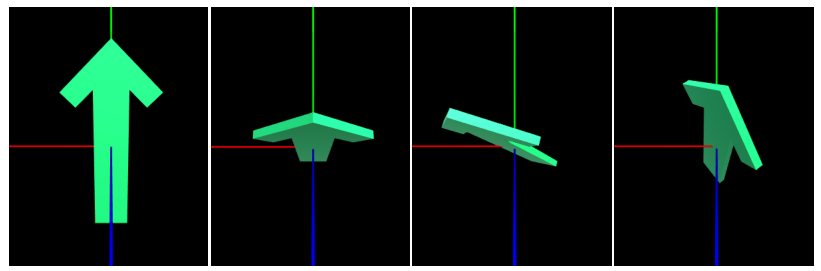
이제 이친구를 y축을 기준으로 회전시켜보자! 예상했을 때는 그냥 부드럽게 y축만으로 내려오는 건데, 그렇지 않고 뭔가 이상한 다른 축들로도 살짝씩 변하면서 움직인다.. 왜그럴까?
Euler transform의 경우, (60, 30, 45)만큼 회전했던 상태에서, y축 기준으로 돌렸을 때의 (x`, y`, z`)으로 3개의 축이 한꺼번에 움직이려고 함.
또 Euler transform의 경우 각도 사이의 보간이 같은 간격으로 보간되지 않는다는 특징이 있음.
그러다보니 하나의 축으로 깔끔하게 회전이 안됨.
2) Gimbal lock
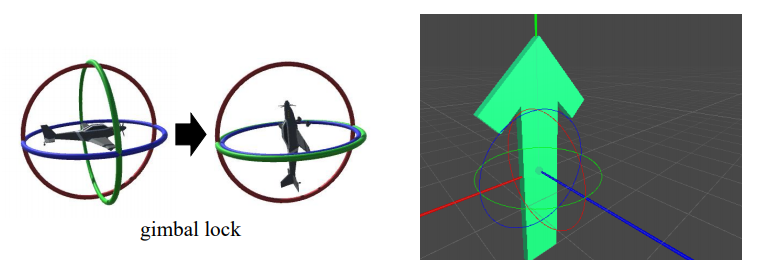
Euler Rotation같은 경우에는 저렇게 축을 잡고 돌리는 느낌으로 생각할 수 있는데,
회전을 하다가, 그림처럼 두 축이 하나로 겹치는 경우가 있음(Gimbal Axis).
그러면 이제 더이상 이 lock을 풀 수가 없어서 한 축에 대한 회전을 아예 구현할 수 없게 되어버림. => Gimbal lock
◆ Quaternion
회전 변환을 나타내는 것이 아닌, "회전된 상태"를 나타냄
Euler angle의 문제점을 해결하기 위해 사용되는 개념이 Quaternion
쿼터니언을 사용해 회전을 표시하면 앞서 말했던 문제들이 전부 해결됨!
쿼터니언은 Euler rotation보다 훨씬 강력하고 효율적이고 문제도 없다. 그러나 알아보기 어려움.
쿼터니언은 4개의 차원으로 표현됨.
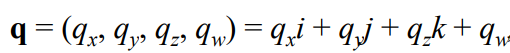
이때 qx, qy, qz는 허수부, qw는 실수부로 표현됨
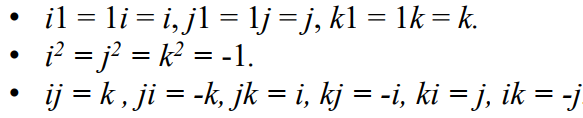
쿼터니언 p, 쿼터니언 q에대해서 pq는 아래와 같이 계산할 수 있음.

Conjugate q* (켤레)의 경우, 허수부에만 -가 붙음
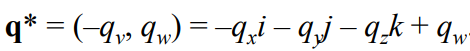
Conjugate 특징
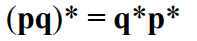
Magnitude

만약 Magnitude가 1인 경우, unit quaternion이라고 하고 다음과 같이 표기함
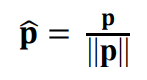
◆ 2D rotation through complex numbers
복소수를 이용해 회전을 표현하는 방법!

우선, p(x, y)를 Rotation Matrix로 θ만큼 돌렸을 때 결과는 위와 같다. (xcosθ - ysinθ, xsinθ + ycosθ)
그런데 이걸 복소수를 이용해서 표현할 수도 있다고 한다!
우선, (x, y)를 복소수 개념을 도입해 x + yi로 정의하자.
그리고, q = cosθ + sinθi라는 unit length 복소수(unit quaternoin)도 하나 정의하자. (cos²θ + sin²θ = 1 이므로)
p와 q를 곱해주면 다음 결과가 나온다.
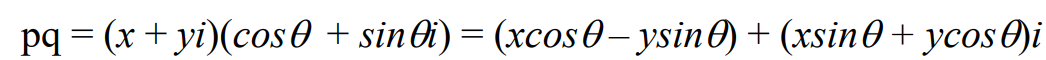
어? 이거 아까 회전 행렬 돌린 값이랑 같은데!?!!
unit quaternion q를 사용하면 쿼터니언의 회전을 표현할 수 있구나!!!
◆ 3D rotation through complex numbers
이번엔 3차원에서 해보겠다. 3차원에서 이 회전을 표시하는 건 살짝 더 복잡함.
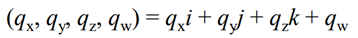
일단 먼저 이 식! 아까 살펴봤던 쿼터니언과 동일하다.
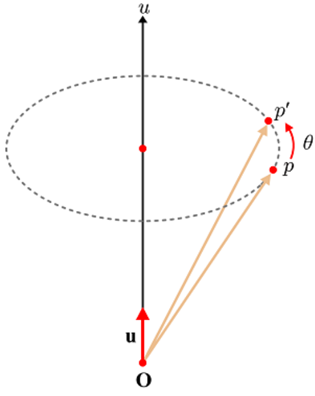
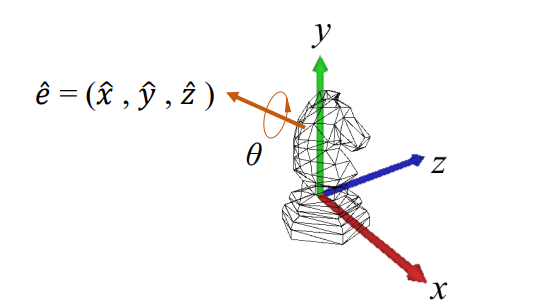
3D vector p, 축 u, 각도 θ가 있다고 하자.
먼저, 점 p를 이용해서 쿼터니언 p를 만들자.
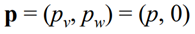
p_v가 점 p에 해당하는 정보 (x, y, z)를 의미한다. p_w는 일단 0으로 두자.
이제, unit quaternion q를 만들어야 함. u와 θ를 이용해서 만든다!
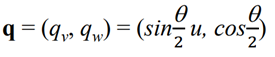
(이때 u는, normalized된 u를 의미함.)
p와 q를 구했다!
이로부터 qpq*를 계산하면, 결과의 imaginary part가 곧 rotated vector가 된다.
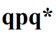
결론부터 얘기하자면 pqp*는 다음과 같다.
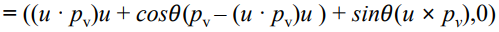
[증명]
p = (p_v, p_w), q = (q_v, q_w)라고 하자.

=> qp를 Eq.1과 같이 표현 가능하다!
우선 cross product p_v × q_v계산하고.
p_w와 q_w는 상수이기 때문에, (q_w)(p_v) = (q_w)(p_x)i + (q_w)(p_y)j + (q_w)(p_z)k 이렇게 표현 가능.
계산해서 묶어주면qp를 Eq.1과 같이 표현 가능하다!
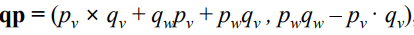
이제 qpq*를 구해보자.
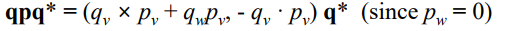
qp = Eq.1 을 넣자. 근데 이때, p_w는 0으로 설정했었기 때문에 p_w가 곱해지는 해당하는 항을 지울 수 있다.

conjugate q이기 때문에, q의 허수부인 q_v에 -를 곱해준다.
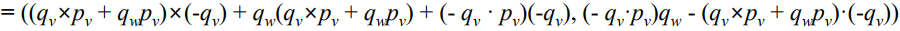
Eq.1에서 했던 것처럼 똑같이 이렇게 만들어줄 수 있다.
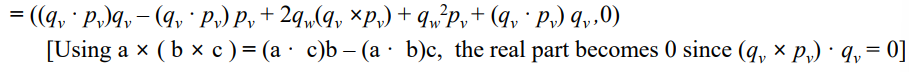
cross product 부분 몇개를 dot product를 사용한 표현으로 바꿔주면, 실수부가 0이 되는 걸 알 수 있음.
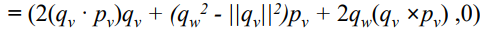
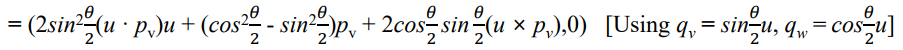

쭉 정리해주면.. 최종적으로 이런 결과 나옴!!
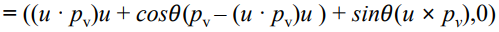
이제 qpq*에 관한 식의 기하학적 의미를 보도록 하자.
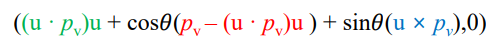
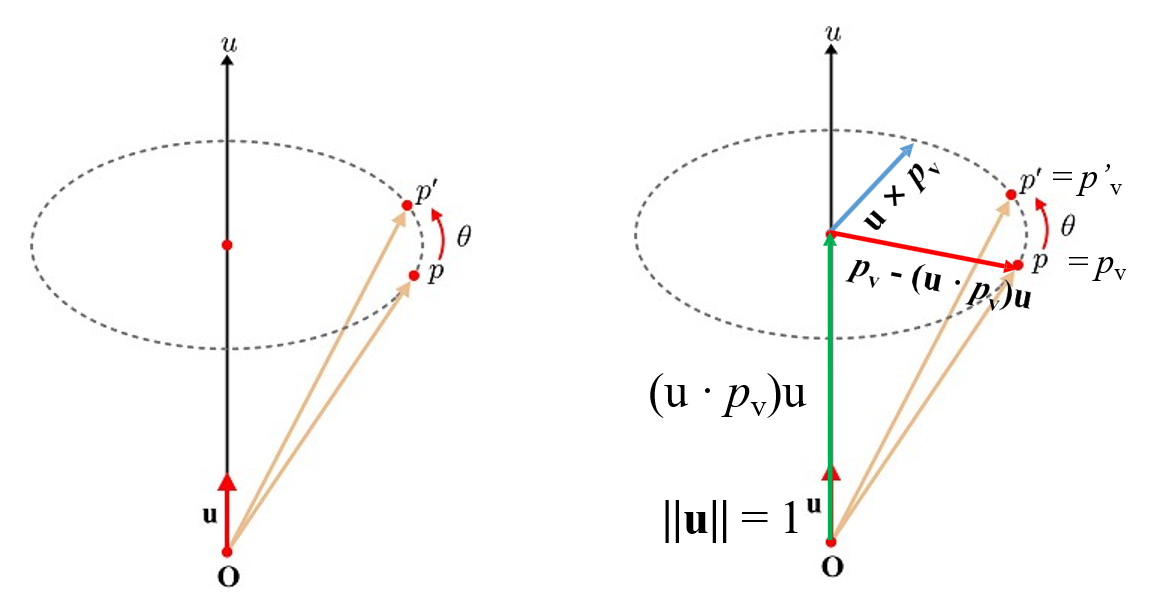
(uㆍp_v)u는, 원점에서 점p까지를 잇는 벡터를 u축에 projection한 벡터.
그림에서 초록색 벡터임
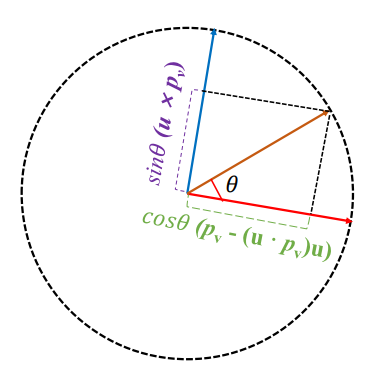
(p_v - (uㆍp_v)u) 는 p_v에서 초록이를 뺀 빨간 벡터인데.
여기다 cos를 취한 cosθ(p_v - (uㆍp_v)u)는 그림과 같이 정사영 내린 길이가 나옴.
θ만큼 돌렸을때의 반지름에다가 빨간 벡터를 projection한 것.
또, (u × p_v)는 cross product 취하면 파란 벡터가 나옴.(u의 방향에 유의)
이는 반지름이므로 위와 같은 방법으로 sinθ(u × p_v)도 얻을 수 있음!
그럼 이 둘(cosθ(p_v - (uㆍp_v)u) + sinθ(u × p_v))을 더하면, 갈색 벡터의 평면상 위치가 나옴.
이게 바로 우리가 돌릴 결과인 p`이다!
여기다가, 원점 O를 기준으로 (uㆍp_v)u 만큼 올라가있으니 더해주면 원점으로부터의 p` 위치 벡터가 나옴~
◆ 3D rotation throung complex numbers - Multiple Quaternions
이제 우리는 qpq*가 어떤 회전을 나타낸다는 것을 알았다.
그러면, 두 개의 회전을 연속으로 하면 어떻게 될까?
p를 q만큼 회전(qpq*)한 다음, r만큼 더 회전을 시켜보자. (r(qpq*)r*)
conjugate 성질에 의해서, 다음과같이 rq에 대한 회전으로 합쳐서 표현할 수 있다.
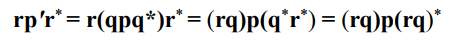
오~ 두 개의 회전을 연속으로 해도, 손쉽게 합쳐질 수 있구나!
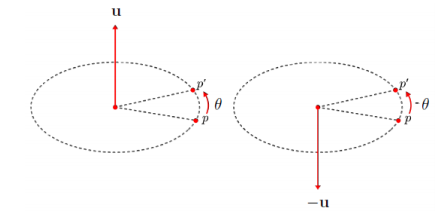
또, u축을 기준으로 θ만큼 회전한 값과, -u축을 기준으로 -θ만큼 회전한 값이 같다는 특징이 있음.
◆ Interpolation of Quaternions
그러면! 쿼터니언은 회전 보간을 해도 괜찮게 나올까?
: ㅇㅇ잘 된다!
회전시키는 '과정 자체'가 쿼터니언이 아니고
'회전된 상태' 가 쿼터니언인 것
현재 쿼터니언과 목표 쿼터니언이 따로 있는 것ㅇㅇ
그래서 깔끔하게 보간도 잘 된다.
◆ Quaternions and Matrix
쿼터니언은 matrix 형태로 바꿀 수도 있당
matrix로 연산하면 빠르니까~
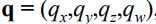
q가 주어졌을 때, 다음과 같은 matrix로 표현될 수 있다.
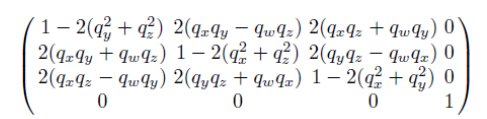
또, matrix가 주어지면 쿼터니언으로 역산할 수도 있다.
위 matrix에서 대각성분을 쭉 더해보자!
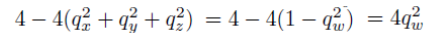
q_w를 구할 수 있음.
또, m₂₁ - m₁₂을 해주면 다음과 같이 q_z를 구할 수 있음.
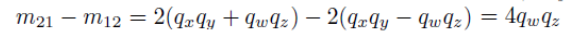
이런식으로 q_x, q_y도 각각 구할 수있을 것임~
결론은, 쿼터니언을 matrix로 표현할 수도 있고,
(쿼터니언을 표현한) matrix가 주어졌을 때 쿼터니언을 다시 역산할 수도 있다! 라는 점~
'게임 > 그래픽 프로그래밍' 카테고리의 다른 글
| 12. Normal Mapping and Tessellation (0) | 2023.05.31 |
|---|---|
| 11. Screen-space Object Manipulation (0) | 2023.05.28 |
| 9. Output-Merging (0) | 2023.05.28 |
| 8. Lighting (0) | 2023.05.27 |
| 7. Image Texturing (0) | 2023.05.26 |




