센로그
11. Screen-space Object Manipulation 본문
화면상 오브젝트 조작에 관한 이야기
◆ Object Picking

우리는 손가락 터치이나, 마우스 클릭을 통해 해당 물체를 선택하기를 원함.
클릭된 위치의 좌표 (x_s, y_s)를 반환하고, 이로부터 물체를 선택해서 그 물체에 대한 조작을 할 수 있도록 ㅇㅇ
이를 위한 기본적인 아이디어는, Ray를 쏘자! 가 된다.

스크린의 점으로부터 z축에 ray를 쏘면, 충돌하는 물체들이 있을 수 있음
그중 가장 처음으로 충돌하는 물체를 선택하자~ 하는 아이디어
근데, 그럼 어디서 찾아줘야 하나?
screen space에서 찾아주면 되나?
ㄴㄴ. 결국 screen space는 렌더링 끝낸 결과물이라, 어떤 오브젝트와 충돌하는지 판단하고 처리를 해주기가 힘듦
따라서 screen space ray를 object space까지 가져가서, 이 ray가 어떤 object와 충돌하고 있구나! 를 찾아주면 된다.
이 과정에 대해 알아보자!
https://grace7040.tistory.com/68 ◁ space transform 에 관한 내용. 참고~
◆ Camera-space Ray
우선, screen space에서의 ray를 camera space로 옮겨보자.

우선, screen상에서 클릭한 시작지점은 camera space에서 near plane 위에 있을 것.
이를 (x_c, y_c, n)이라고 하자. (camera space에서의 x, y, near plane)
camera -> clip space로 보내기 위해 projection matrix를 이용했었음

그리고 clip space -> screen space로 보내기 위해 viewport matrix를 사용했었음.

최종적으로 camera space~> screen space까지 옮겨온 좌표임.
이렇게 옮겨온 좌표가, (x_s, y_s, 0)과 일치해야 한다! (스크린상의 x, y)
이를 통해, (x_s, y_s, 0)과 (x_c, y_c, n) 사이의 식을 도출해보자


이 식을 통해, 우리에게 (x_s, y_s) 좌표가 주어졌을 때, camera space에서의 좌표 (x_c, y_c, n)을 구할 수 있다 ㅇㅇ
이제 우리가 ray를 쏘려면 필요한 것은 direction vector이다.

near plane에 있는 시작점 p의 좌표를 (x_c, y_c, n)이라 할 때
p에서 원점을 뺀 벡터 (x_c, y_c, n) - (0, 0, 0)는 원점으로부터 p까지 잇는 벡터를 의미함.
굿~
이제 우리는 screen space에서 camera space까지 옮길 수 있게 되었다.
◆ World-space Ray
그 다음으로 ray를 보내야할 곳은, world space
원래 world space -> camera space로 올 때 사용했던 것은 view transform이었다.
M_view = TR의 형태를 가졌음.
그런데 이제 반대 과정을 가야하니까! M_view inverse 를 취해주자.

△ 결과 4열이 4행으로 가야함.. 나중에 수정해서 올리겠음
각각의 역변환 행렬을 곱해주면, world space까지 ray를 가져올 수있다.

◆ Object-space Ray
object space 같은 경우, 물체마다 따로 가지고있었다.
원래 object space -> world space로 올 때 사용했던 것은 world transform M_world 였다.
그런데 반대로 해줘야 하니, M_world inverse를 취해줘야함.
이것은 물체마다 다르다는 점을 기억하고 가자.

암튼 각자의 M_world inverse를 곱해주면, ray를 각자의 object space로 가져올 수 있게 됨~
이제 해야하는 일은, 이 ray와 object의 triangle이 충돌하는지를 봐야함
충돌하면 선택하고, 아니면 안하면 되는 것.
근데 문제가 있다!
모든 triangle마다, 충돌했는지 안했는지 체크하기에는 너무 오래 걸릴 것임.
=> 좀 더 빠르지만, 덜 정확한 방법. Bounding Volume (BV)를 이용하는 방법 도입.
◆ Bounding Volume
어떤 물체가 있을 때, 그 물체를 감싸는 간단한 형태의 geometry

ray가 왔을 때, 삼각형 하나하나 충돌하는지 체크하는 게 아니라 BV 기준으로 체크함 => cost 감소!
BV에는 크게 두가지 종류가 있다.
- AABB(Axis-Aligned Bounding Box)
- Bounding Sphere
AABB 같은 경우, object space의 x축, y축, z축 (주축; principal axis)위에 어디서부터 어디까지 존재하는지 표현함.
그러면 큐브 형태가 생성될 것이고, 이 큐브를 기준으로 ray가 충돌했는지 아닌지 판단함.
Bounding Sphere 같은 경우, 영역으로 하는 것이 아닌 중심점(center)과 반지름(r)을 이용해서 계산함.
우리는 ray의 시작점과 방향을 알기 때문에, 다음과 같이 각 component들에 대해 수식을 세울 수 있다.

그렇게 세운 수식을 bounding sphere 공식에 대입!

여기서, 해가 몇개인지 (0, 1, 2) 체크하면 충돌 여부를 판단할 수 있음!

참고)
ray-sphere intersection test는 우선 preprocessing 과정에서 자주 수행된다.
500명이 있는 게임에서 총을 쏘는 경우, 다 정밀 체크하기엔 너무 많아!
=> BV에 맞은 사람 몇 명 추려낸 다음에 그 사람들에 한해서만 정밀 체크하도록 할 수 있음.
◆ Ray-Triangle intersection
이제 BV를 통해서 맞을 것 같은 사람 몇명 추렸다!
정확한 체크를 위해서, 삼각형 기준으로 충돌을 체크해봐야 함
Triangle <a, b, c>가 있고, 얘가 p점에서 ray를 맞았다고 하자.

그러면 이 triangle이 3개의 sub traingle로 나뉠 것임. 이를 이용해서 맞았는지 체크함

나뉜 삼각형 넓이/전체 삼각형 넓이 를 각각 u, v, w로 정의하자
만약 p가 정말로 삼각형 안에 있다면, 다음 수식들을 만족해야 한다.
- u + v + w = 1
- p의 좌표 = ua + vb + wc
이때 w = 1 - u - v를 대입하면

p를 이렇게 u, v 두가지로 나타낼 수 있다.
이제 위 식을 활용해보자.
p는 앞서 언급했듯 시작점 s로부터 td만큼 더한 s+td로 표현할 수 있다.
또 p는. a, b, c 세 점과 각 비율을 곱해서 더한 ua + vb + wc, 즉 ua + vb + (1-u-v)c 로도 표현할 수 있다.
둘을 엮어보자!

양 변을 정리해주면

상수항들을 c-a = A, c-b = B, c-s = S로 치환해서 예쁘게 만들어주면

이런 형태가 이제 각각의 x, y, z에 대해 나올 것임.

이런 형태의 경우 Cramer's Rule을 통해 간편하게 풀 수 있음.

※ Cramer's rule 풀이
Ax = B 형태로 모델링해서 풀면 잘 풀리는 경우가 많음
Cramer's rule에서도 이런 형태로 바꿔주고 공식으로 풂

이걸 풀면 u와 v의 값을 알 수 있을 것! 이때 한번 더 체크해줘야할 사항이 있음
다음 제한조건을 만족하는지 체크해줘야 함
- u ≥ 0
- v ≥ 0
- u + v ≤ 1 (두 삼각형을 합한 넓이가 전체 삼각형보다는 작거나 같아야 함)

p가 삼각형 밖에 있는 경우 u + v > 1
또, ray가 한 오브젝트에 여러번 충돌하는 경우도 있을 것임!

그런경우 smallest positive t를 선택하면 됨
◆ Rotating an object
우리가 오브젝트를 선택했다. 이제는 손가락을 움직여서 선택한 물체를 돌리는 경우에 대해 생각해보자.
2D screen에서 손가락을 움직여서, p1~pn까지 옮겼다고 하자.
이때 {p1, p2, ... , pn}과 같이 그 움직임을 추적할 수 있을 것임. 이걸 사용해서 물체를 돌려보자.

◆ Rotating an object - Arcball
Arcball이라는 개념을 도입한다. 이는 돌릴 오브젝트를 감싸고 있는 가상의 구이다.
우리가 선택한 오브젝트를 돌리는 행위는, Arcball을 굴리는 행위와 똑같다고 가정한다.

그리고 좀더 쉬운 계산을 위해, 2D screen을 2x2 square로 normalize한다.
Arcball을 unit sphere로 사용하기 위함! (반지름 1)
이에따라 충돌점 p_i와 p_i+1도 q_i와 q_i+1로 바뀌게 될 것임.

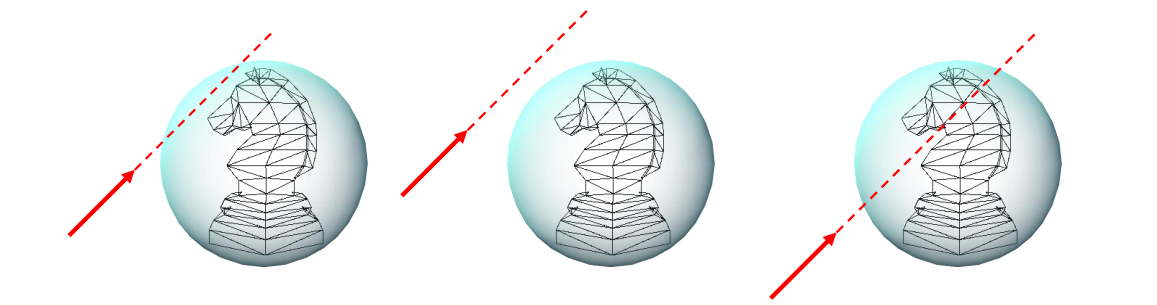
우리가 손가락으로 화면을 클릭한 점을 q라고 하자. 이를 먼저 Arcball 위로 z축을 따라 projection 시킨다.
z축값만 변경되었으므로, q_x와 q_y는 변함 없음. 따라서 v_x = q_x, v_y = q_y이다.
또, 구 위의 한 점 v에 대해 다음이 성립한다.

이를 통해 v_z까지 구할 수 있다.

만약 그림과 같이, q를 projection한 v가 arcball의 바깥에 있다면, 즉 (q_x)² + (q_y)² > 1이라면
그냥 v를 normalize시켜서 구 안에 있도록 함. v = normalize(q_x, q_y, 0)
이제 이동 측면에서 보자!

v_i와 v_i+1이 주어졌을 때, 어떻게 회전시켜야 하는가?
이때 필요한 게 두가지가 있다.
- rotation axis : 무엇을 기준으로 회전시킬 것인가?
- rotation angle : 얼마나 회전시킬 것인가?
rotation axis같은 경우에, v_i와 v_i+1을 cross product 해주면 axis가 나옴.
rotation angle 같은 경우에, v_i와 v_i+1을 dot product 해주면 나옴.
그러면 이제 어떤 축을 기준으로 얼마나 회전시켜야 하는지 알 수 있다!!
◆ Rotating an object - Arcball↔Object space Rotation Axis
우리는 방금 어떤 축을 기준으로 얼마나 회전시켜야 하는지 얻었다.
그러나 이건, Arcball이라는 가상의 space 상에서 얻은 것임!
그러므로 이걸 object space로 보내줘야 할 필요가 있음.
원래 우리는 Arcball이라는 게 카메라 너머에 있다고 가정했었음.
따라서 그냥 camera space에 있다고 가정해도 됨 ㅇㅇ
그러면 아까 ray picking시 space 변환 했던 것처럼, camera space -> world space -> object space로 변환할 수 있을것임.

유의할 점은, 이 회전은 다른 world transform이 적용되기 전에 먼저 적용되어야 한다.
당연함. 먼저 돌린 상태에서 다른 변환을 해줘야함~
이 변환을 R이라 할 때, M_world 변환을 할 예정일텐데
RM_world 형식으로 먼저 해줘야 한다는 뜻~ (DirectX 기준)
또 이런식으로 변환을 해준 상태에서 또 손가락을 움직이면, 또 역변환 과정을 거쳐야 할 것
그러면 이번에는 M_world inverse가 아닌 RM_world inverse로 구해줘야함.
이런식으로 쭉~ 클릭 또는 터치에 따른 object 움직임을 구현할 수 있다.
'게임 > 그래픽 프로그래밍' 카테고리의 다른 글
| 13. Character Animation (0) | 2023.05.31 |
|---|---|
| 12. Normal Mapping and Tessellation (0) | 2023.05.31 |
| 10. Euler transforms and quaternions (0) | 2023.05.28 |
| 9. Output-Merging (0) | 2023.05.28 |
| 8. Lighting (0) | 2023.05.27 |




