센로그
12. Normal Mapping and Tessellation 본문
◆ Bumpy surface

벽돌 벽이나, 포장 도로는 우둘투둘한 표면(Bumpy surface)임. == 우둘투둘한 곳에 vertex가 존재한다는 의미.
당연히 전부 고해상도로 렌더링하면, 현실과 비슷해 보일것임 ㅇㅇ 그러나, 너무 비쌈.

렌더링을 위해, data bus를 통해 CPU => GPU로 데이터 전송을 하고, GPU 파이프라인 내에서 처리를 하게 됨.
이때 vertex 개수가 많을수록 한번에 넘어가야 하는 데이터 개수와, Gpu내에서 처리해야 하는 데이터 양이 많아짐
=> 우둘투둘한 표면에 대한 고해상도 폴리곤 메쉬를 처리하기 어려워짐!!
※ GPU에 올려놓고 연산 처리하는 과정 :
사실 이 과정은 GPU 성능에 따라 빠르게 할라면 빠르게 할 수 있으니까 괜찮다 치자.
반면 CPU => GPU 옮기는 과정은 물리적인 과정이라 더 빠르게 하기 어려우므로, 넘기는 부분만 어떻게 잘 처리해주면 됨.
※ CPU => GPU로 데이터 전송(data bus) 과정 :
High resolution polygon mesh를 사용하면 이 과정에서 bottleneck이 존재함. 근데 테셀레이션(Tessellation) 쓰면, 일단 이 과정에서 low resolution으로 넘기고, GPU에서 처리함으로써 data bus 전송 과정의 데이터량을 줄여줌. 굿
그러면, 별로 안 비싼 low resolution mesh를 써보는 건 어떨까?

... 아까에 비해 확실히 퀄리티가 많이 떨어짐.
빛을 쬐어줘도 뭔가 이상함.
그 이유는 normal data 때문임.

빛 계산시 surface normal과 light의 방향을 사용하는데,
아무래도 low resolution 같은 경우에는 normal이 전부 위로만 향해있기 때문에 빛에 비췄을 때 어색함.
따라서 고해상도와 저해상도 mesh 사이의 절충안을 찾아야 한다!!!!
◆ Normal Mapping
핵심 아이디어는 pre-computed normal을 사용하겠다! 라는 것이다.

high resolution일 때의 normal을 계산해서, (float) texture로 만들어 줌.(normal map)
하나하나가 normal의 방향을 갖고있는 것.
실제로 렌더링 할 때는 low resolution mesh를 넣고, 미리 저장해놓은 high resolution normal map을 입힌다.
이전처럼 normal 하나하나 계산해서 쓰는 게 아니라, normal map에있는 정보를 가져다 쓴다는 것.
짠~ 결과!

확실히 low resolution보다는 훨씬 어색한 느낌이 사라졌다.
vertex 개수를 증가시킨 것이 아닌데도 퀄리티가 좋아졌다!!
◆ Normal Mapping Generation
구체적으로 어떻게 하는지 살펴보자.

우선 image texture를 height map으로 바꿔주는 과정이 필요함
울퉁불퉁한 질감을 표현하기 위해, 우선 이친구한테 필요한 건 높낮이 정보이다.
즉, 얘가 지금 위로 올라와있는지 아래로 내려가있는지에 관한 정보. 이걸 height data (elevation data)라고 부름
이런 데이터를 표현하고 있는 map을 height map이라고 부름
[0, 255]까지 사용해 높낮이를 표현함. (0에 가까울수록 낮음. 검정색)

height map을 이용해 normal map을 만들 수 있다!
그림에서 (x,y)에서 normal 을 구하기 위해, 주변 점 몇 개(여기선 4개)를 참조해서 구함.
Q. 그럼 모서리에 있는 애들은 어떡해요? 참조를 못하자나요.
A. 끝 영역에서는 대충 무시하거나, 테두리에 가상의 데이터를 만들어서 함
아니면, UV coordinate에 0.99 곱해서 작게만들어서 계산한 후 키우는 흑마법씀ㅋㅋ
이렇게 얻어진 normal 성분들은 [-1, 1]의 범위(벡터는 왼쪽이 -면 오른쪽은 +니까)를 갖는 floating point 형식(벡터 값을 정확히 표현하기 위함)이다.
그런데 지금까지 우리가 알던 텍스처는 -가 존재하지 않았음! image viewer 같은 것에서도 negative color가 존재하지 않음.
따라서 RGB 범위가 [0, 1]인 texture에 normal을 저장하고 싶다면, 다음과 같이 범위를 맞춰줘야 함.

만약 쓰고있는 normal map이 이미지 파일 png 같은걸로 되어있다? 그럼 –가 없는거임
그러면 사용할 때 다시 [-1, 1]로 바꿔줘야함 ㅇㅇ(시스템별로 지정된 normal map 형식에 맞게 바꿔줘야 한다는 뜻)
◆ Normal Mapping - 사용법

polygon mesh가 rasterized되어 나온 texture 좌표 (s, t)가 normal map 접근에 쓰인다고 하자.
(s, t)에서의 normal은 normal map을 필터링(mesh와의 크기 맞추기)함으로써 얻어짐.
이것을 diffuse reflection term에 넣어서 계산한다고 치자.
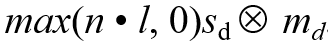
normal n은 normal map에서 가져온다.
=> 이때 Vertex shader(VS_INPUT)로부터 넘어온 normal map이 아닌, 고해상도 텍스처로 부터 얻은 normal map을 사용함!
m_d (material_diffuse)는 image texture로부터 가져온다.
이렇게 하면, low resolution일 때보다 훨씬 현실적인 결과가 나온다!!

◆ Normal Mapping - 특수한 경우
Normal mapping 한다는 것은, texturing한다는 소리다.
texturing이라는 건 포장지를 펴 바르는 것과 같다고 했다.
평면에 바를때는 쭉 펴면 되니까 쉬움.
그런데...

이런 특수한 형태에 입히면?
그림처럼 normal이 뭉칠 수 있다. 따라서 특별한 처리가 필요하다.
=> Tangent space Normal Mapping
◆ Tangent-space Normal Mapping

빛의 효과를 계산할 때, normal 과 light의 dot product 과정이 포함된다.
(실제로 앞서 우리는 diffuse lighting을 계산하기 위해 normal과 light의 dot product를 구하려고 했었다.)
그런데! 사실 일반적으로 이건 동작 할 수 없음.
왜냐하면, normal은 tangent-space vector이고, light는 world-space vector 이기 때문.
※ 그럼 아까 평면에서는 왜 잘 작동했냐?
평면에서는, tangent space basis와 world space basis가 일치했기 때문에
light와 n(s,t)의 space가 달라도 결국 같은 기저를 쓰는 공간이기 때문에 연산에 문제가 없었다.
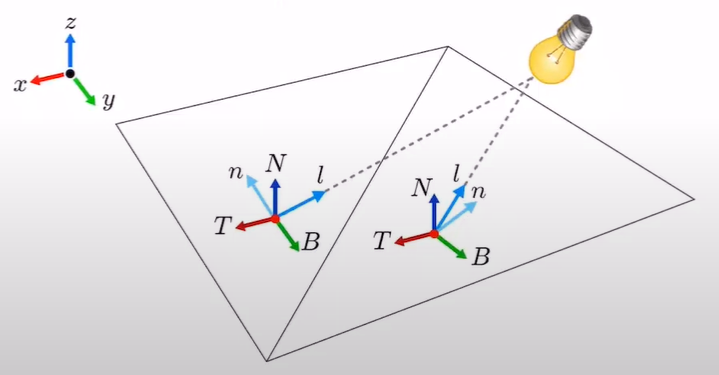
그러나 평면이 아닌 경우, 표면의 점들에 대한 tangent space의 basis가 달라짐
=> light와 n(s,t)가 다른 공간에서 정의된 것임!!
따라서 연산을 위해서는 공간을 일치시켜 줘야 한다는 것.
Tangent-space란?
표면의 한 점에서 정의되는 공간으로, 다음 세개의 정규직교(orthonormal) 벡터로 정의된다.
- T (tangent)
- B (bitangent)
- N (normal)

그림과 같이, 구의 한 점 p 또는 q에 대해 T, B, N이 각각 정의된다. (구의 모든 표면점에서 정의됨)
p 점에 대해서 살펴보자.
Np은 p에 대한 Tangent space에서 정의된 normal vector임. (0, 0, 1).
normal mapping을 안 쓸거면, 그냥 Np를 갖다 써서 계산하면 됨.
그런데 normal mapping을 쓸거면! Np대신, n(sp, tp)를 써야함.
n(sp, tp)는 p 지점에서의 texture 좌표 (sp, tp)를 이용해서 normal map을 필터링해서 얻어온 normal vector를 의미함.
얘는 항상 Np을 약간 rotation한 형태라서, "p의 tangent space 에서 정의된 벡터라고 볼 수 있다" 는게 핵심.
암튼 이제, n(s, t)가 tangent space에서 정의된 벡터라는 걸 알았다.

normal은 tangent space vector이고, light는 world space vector라고 했었다.
normal과 light를 연산하기 위해서는, space를 통일시켜줘야 함.
즉, normal을 world space로 보내거나, light를 tangent space로 갖고 와야함.
우리는 후자를 사용할 것이다.
◆ Tangent-space - Matrix_TBN
그러려면 Tangent space를 계산하기 위한 matrix를 만들어야 겠죠?
{T, B, N} 이라는 matrix를 만들거야.

이 중에서 N은, modeling stage에서 정의된 거라 걍 VS_INPUT에서 갖고오면 됨.
그럼 이제 T와 B를 구현해야 함.

우선 T를 구한다고 하자. 표면에서 평행한 벡터들로 구현할 것임.
그런데, 표면에서 평행한 벡터들이 그림처럼 360도 돌면서 쭉~ 있으니까 너무 많아!
=> 그중에서 그냥 하나를 뽑을거야. 그냥 texture coordinate의 basis와 일치하는 벡터로 뽑자!

같은 방식으로 B도 뽑을 수 있을 것임.
이게 구체적으로 어떤 방식이냐면! 일단 구체적 과정은 다음과 같음.

=> 결론적으로 T를 U로, B를 V로 일치시켜서 T 벡터, B 벡터를 구해온 것임.
사실.. vertex shader에게 그냥 TBN을 줘버리면 됨.
결국 TBN은 object space에서 정의된 녀석들이기 때문에, vertex shader은 얘네를 world space으로 transform 할 것임.
그러면 우리는 world space에서의 TBN을 알게 되기 때문에, 이로부터 손쉽게 object space로 되돌리는 행렬을 구할 수 있음. (rotation 역변환 했던 거 기억. 그냥 전치시켜주니까 됐었음)

이렇게 해주면 됨~ 위에서 계산한 거랑 똑같음 ^^
이제 이렇게 나온 행렬을 world space의 light vector l에게 곱해줌으로써 l을 tangent space로 옮겨올 수 있다!!

결과적으로, 이상한 도형에서도 normal mapping을 통해 이런 느낌이 표현이 가능하다~ 라는 점!
◆ Normal Mapping Discussion
normal map은 space에 따른 두 가지 종류가 있다.
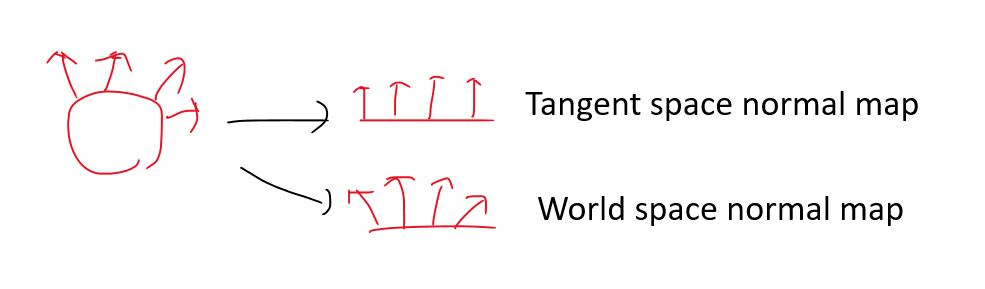
- Tangent-space normal map
- World-space normal map
우리가 다룬 건 Tangent-space normal map이다. 얘의 장단점을 살펴보자.
장점)
- world상에서 object의 방향이나 position에 상관없이 사용할 수 있기 때문에, reuse하기 좋다.
- characker skin과 같은 deforming(변형되는)한 표면에서도 잘 작동한다. normal이 world에 대해서가 아닌, object의 표면 자체에 대해서 상대적으로 계산되기 때문임.
단점)
- 일관된 tangent 공간을 계산하고 유지해야 하며, 모델 생성 및 쉐이딩 계산에 복잡성이 추가됨.
- UV 좌표가 분리되거나 기하학적으로 대칭인 부분에서 선이 생길 수 있는 문제
암튼 general하게 잘된다~
◆ Hardware Tessellation
이제 테셀레이션에 대해 살짝 맛보기 시간~

필기가 상당해서 캡쳐해옴
Hardward Tessellation은 GPU가 primitive를 더 작은 primitive들로 분해하는 것을 의미함.
Tessellation은 Hull Shader => Tessellator => Domain Shader 순으로 진행함.
- Hull Shader : 어디에 어떻게 정점을 추가할지 계산해 결정한다.
- Tessellator : Hull Shader에서 받아온 정보로 실제로 정점을 추가한다.
- Domain Shader : 새로 만든 정점들에 대한 transform 연산을 수행한다.
이중 Hull shader, Domain shader은 programmable한 것이고
Tessellator은 내부에서 어떻게 동작할지를 미리 만들어진 하드웨어 function이다.
◆ Displacement Mapping
우선 Displacement mapping에 대해 이해가 필요하다!
사실 Normal mapping에도 단점이 존재함. 실제로 geometry 자체를 바꾸는 게 아니기 때문임.

저런 구에다 적용하면 눈속임인 거 엄청 티남. 표면 자체가 바뀌진 않기 때문에 디테일의 한계가 존재함.
반면 Displacement mapping은, vertex가 실제로 움직이는거라 geometry가 실제로 변함
어떻게 하면 좀더 실제처럼 구현할 수 있을까?
=> 우선 tessllation을 이용해서, base surface를 잘게 쪼갠다. Vertex들을 생성하면서, 삼각형을 잘게 쪼갬.
=> 이렇게 tessellate된 vertex들을 이동시켜서 디테일을 표현하는 거 자체를 displacement mapping이라 함
◆ Tessellation 과정

input은 patch 또는 base surface라고 부름. triangle이거나 quad 중 하나임.
포장 도로 예시를 들어보자. Hull shader가 quad를 base surface로 받고, 최종적으로 Domain shader까지 넘김.
- Hull Shader는 tessellation level을 결정함. 즉 이거 어느정도 레벨로 쪼개줘~ 를 결정하고, Tessellator에게 넘김.
- Tessellator은 이에따라 실제로 쪼갬. quad 영역을 2D triangle mesh로 쪼개서 Domain Shader에게 넘김.
- Domain Shader은 2D mesh의 각 vertex마다 실행됨. quad를 bilinear patch로 취급하고 (u, v)를 이용해 (x, y) 값을 계산함. 그리고 height map의 높이대로 z값을 정함.(해당 지점의 높이를 z 만큼 올림)
◆ Hull Shader
HS는 tessellator가 요구하는 정보들을 정의해줌.
- 이 정보들에는 control point 개수, patch face 타입, tessellating시 사용할 partitioning type 등이 있음.
- tessellation factor도 여기서 정의됨.
■ Vertex Shader(VS) & Hull Shader(HS)
HS가 들어오면 VS는 더이상 space change를 다루지 않는다!
- VS의 가장 큰 역할은 space change를 해가면서 vertex들의 최종 position을 계산해주는 거였음.
- 그러나 Tessellation을 구현하려면 Vertex들을 생성해주는 단계가 있으므로, clip space까지 보내면 안됨. (object space 에서 처리해야 함). 그래서 Domain Shader까지 옮겨가서, space change까지 수행해줌!
◆ Tessellator
Tessellator는 patch를 더 작게 나눠서 barycentric coordinate(무게중심 좌표)들을 생성해서 DS에 넘김.
Tessellator는 항상 single input(vertex)과 single output(barycentric coordinate)을 갖는다는 점에서 VS와 유사하다.
Tessellator는 한번 시행할 때 하나 이상의 vertex를 생성하거나 삭제할 수 없다. (하나씩만 가능)

barycentric coordinate란, 실제 좌표계가 아니라 대충 내부에서 0, 1 이런 식으로 보고 내부에 정점을 찍는 것.
말그대로 무게중심 느낌. 어느정도 떨어져있는지.

Inner tessellation level과 outer tessellation level에 맞게 정점의 barycentric coordinate를 추가한다~
맨 왼쪽 그림에서 Inner은 5였는데, Outer은 7로 늘어난 것을 볼 수 있음.
맨 오른쪽에 보면 결과로 7등분 되어져있음ㅇㅇ
◆ Domain Shader
tessellator 로부터 받은 vertex position을 bilinear patch의 control point로 쓴다.
(u, v, w)를 이용해서 3D point(좌표)를 도출한다. 해당 space에서 필요한 좌표계를 생성하는 것.
texture 좌표계 역시 같은 방식으로 bilinearly하게 보간된다.
tessellator 단계에서 넘어온 좌표마다 한번씩 수행한다.

◆ Displacement Mapping
결과물~

'게임 > 그래픽 프로그래밍' 카테고리의 다른 글
| 14. Shadow Mapping (0) | 2023.06.09 |
|---|---|
| 13. Character Animation (0) | 2023.05.31 |
| 11. Screen-space Object Manipulation (0) | 2023.05.28 |
| 10. Euler transforms and quaternions (0) | 2023.05.28 |
| 9. Output-Merging (0) | 2023.05.28 |




