센로그

정렬 문제의 계산 복잡도는 O(n lg n)이라는 걸 7장에서 증명했었다. 이번에는 검색 문제에 대해서 알아보자! ◆ 키를 비교함으로만 검색을 수행하는 경우의 하한 검색 문제란, n개의 키를 가진 배열 S와 어떤 키 x가 주어졌을 때, x = S[i]가 되는 인덱스 i를 찾는 것. 만약 x가 배열 S에 없을 때는 오류(F)로 처리한다. 이분 검색의 경우, 시간복잡도가 W(n) = floor(lg n) + 1이 되는데, (floor은 바닥 함수를 의미함) 정렬되어있을 때 키를 비교함으로만 검색을 수행하는 경우 이분 검색보다 더 좋은 알고리즘은 없다! 이진 검색과 순차 검색의 결정 트리를 비교하면서 이를 살펴보자. ■ 이진 검색의 결정 트리. 큰 마디(내부마디) – 키와 각 아이템을 비교하는 마디 작은마디(..

◆ 계산 복잡도문제가 갖고있는 본연의 계산량. 최소한 얼마나 많은 계산을 해야 그 문제가 풀리는지문제풀이 접근하는 2가지 방법(1) 문제를 푸는 더 효율적인 알고리즘을 개발 (2) 더 효율적인 알고리즘 개발이 불가능함을 증명 (예) 정렬문제인 경우 Θ(n log n) 보다 좋은 알고리즘은 불가능함이 입증 되었음. 일반적으로  “계산 복잡도 분석”이란  “문제의  분석”을  지칭 (not "알고리즘의 분석")어떤  문제에  대해서  그  문제를  풀  수  있는  모든  알고리즘의  효율의  하한(lower-bound)을  결정한다.(최소한 이것보다는 오래걸리거나 비슷하게 걸린다.) ex) 예를들어 행렬 곱셈 문제를 보자.- 알고리즘의 분석✓ 일반알고리즘: Θ(n³)✓ Strassen의 알고리즘: Θ(n^..

◆ 분기 한정법 (Branch and Bound)Branch: 가지를 나눈다Bound: 한계를 정한다 내가 어느쪽으로 가는 게 더 이득인지 가지를 치는 과정에서 한계를 가지고 판단하겠다 라는 뜻 되추적의 개념 + 최적화 문제에 대한 가장 좋은 해를 찾는 개념이 포함되어있다.기본적으로 해를 찾아가는 방법은 백 트래킹.어떤 해를 선택하느냐는 bound를 사용하며 뭐가 더 이득인지 판단. 되추적에서는 상태 공간 트리를 움직이면서 해를 찾았음. (promising 함수 사용)분기한정법에서도 상태 공간 트리를 순회하긴 하는데, Bound 함수를 통해서 지금까지 찾은 해보다 최대한 더 좋은 해를 찾는 방향으로 나아가며, 최종적으로 가장 좋은 해를 찾아나가는 방법.  ◆ 최소화 문제최소 거리의 트래킹 코스를 찾는 문..

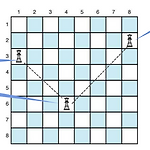
◆ 되추적!? 어떤 수에서 더이상 확장할 수 없거나 유망하지 않다면 전 단계로 돌아가면서, 상태 공간을 만듦. 그 상태공간을 돌아다니면서 해를 찾는 방법. 마디의 유망성: ✓ 전혀 해답이 나올 가능성이 없는 마디는 유망하지 않다(non-promising) ✓ 그렇지 않으면 유망하다(promising). 되추적이란? ✓ 어떤 마디의 유망성을 점검한 후, 유망하지 않다고 판정이 되면 그 마디의 부모마디(parent)로 돌아가서(backtrack) 다음 후손마디에 대한 검색을 계속하게 되는 절차. ✓ 부모마디로 돌아가는 것 → 가지치기(pruning) ✓ 이 과정에서 방문한 마디만으로 구성된 부분트리 → 가지친 상태공간 트리(pruned state space tree) ◆ 트리 방문 순서 ◆ n-queens ..

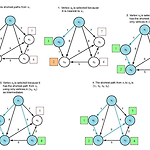
◆ Dijkstra 알고리즘하나의 출발 지점으로부터 다른 모든 도착 지점들로 가는 각 최단 경로들을 모두 계산할 때 쓰는 방법F (최종 결과 엣지 집합)를 공집합으로 초기화Y (최단 경로가 확정된 노드들 집합)는 출발 노드로 초기화.(예시에서는 v1에서 출발하는 걸로 가정)V-Y집합(최단 경로가 확정된 노드들을 제외한 노드들)에 속한 노드 중에서, v1(출발 노드)에서 Y에 속한 정점만을 거쳐서(무조건 거쳐야 하는 것은 아님) 최단 경로가 되는 정점 v를 선정한다.그 정점 v를 Y에 추가한다.v에서 Y로 이어지는 엣지('v와 Y를 잇기 위해 Y내에서 최종 경유하는 노드'와 'v노드'간의 엣지)를 F에 추가한다.Y = V가 되면(전체 노드 다 돌음), T = (V, F)가 최단 경로를 나타내는 그래프(ve..

◆ 탐욕적인 알고리즘 (Greedy Algorithm) 이란?현 단계(상태)에서 가장 좋다고 생각되는 답을 선택함으로써 최종적인 해답에 도달하는 방법. 현 시점의 가장 좋은 해는 local 최적해이다. 그러나 항상 이것들이 모여서 global 최적해를 만들진 않는다.따라서, 탐욕적인 알고리즘을 사용하려면 항상 최적의 해답을 주는지를 반드시 검증해야 함! ◆ 탐욕적인 알고리즘 설계 절차걍 이런게 있구나 알고, 실제 알고리즘에서 어떤 부분이 어느 단계에 속하는지 알면 됨 1. 선정 과정 (selection procedure)  현재 상태에서 가장 좋으리라고 생각되는(greedy) 해답을 찾아서 해답모음(solution set)에 포함시킨다. 2. 적정성 점검 (feasibility check)  새로 얻은 ..