센로그
1장. 알고리즘: 효율, 분석, 그리고 차수 본문
◆ 알고리즘의 정의
문제를 해결할 수 있는
1) 잘 정의된, 2) 유한시간 내에 종료되는, 3) 계산적인 절차
1) well defined: 잘 정의 되었다는 것은 a가 설명했으면 b가 그걸 정확하게(다르게 해석되지 않게) 이해할 수 있는 것.
2) finite : 언젠가는 끝나는 게 보장되어야 함
3) computational: 입력을 받아서 출력으로 전환시켜주는 일련의 계산 절차.

알고리즘은 프로그램의 엔진에 해당하는 중요한 절차이다!!
◆ Algorithm vs Method
Algorithm은 유한 시간 내에 종료됨
Method는 유한 시간 내에 종료되는지 모름
◆ 문제의 표기 방법
- 문제
답을 찾고자 던지는 질문 - parameter 매개변수
문제에서 특정 값이 주어지지 않은 변수 - instance 문제의 사례
파라미터에 특정 값을 지정했을 때의 사례 - solution 사례에 대한 해답
주어진 사례에 관한 질문에 대한 답
◆ 알고리즘의 표기 방법
ㆍ자연어
그냥 말로 설명해주는 것. 정확히 전달되지 않을 수 있음
ㆍ프로그래밍언어
정확하게 기술할 수는 있지만, 너무 어렵고 복잡
ㆍ의사코드(Pseudo code)
프로그래밍 언어는 아니지만 이와 유사하게 표현. (우리는 이걸 많이 쓸 예정!)
ㆍ흐름도
◆ 알고리즘의 정확도 분석
알고리즘이 의도한 대로 수행되는지를 증명하는 절차
정확한 알고리즘이란 모든 입력에 대해 유한시간 내에 정확한 답을 출력하는 알고리즘
(정확하지 않은 알고리즘이란 무한시간 or 정확하지 않은 답 출력)
◆ 알고리즘의 복잡도
알고리즘의 복잡도를 어떤 방식으로 표현할지에 대한 이야기.
ㆍ공간 복잡도(space complexity)
입력 크기에 따라 메모리가 얼마나 필요한지 결정하는 절차
ㆍ시간 복잡도(time complexity)
입력 크기에 따라 단위연산이 얼마나 수행되는지 결정하는 절차
(단위 연산이란 비교문, 지정문 등을 의미함)
◆ 알고리즘 분석 방법의 종류
1) 모든 경우 분석 Every-case analysis
2) 최악의 경우 분석 Worst-case analysis O
3) 평균의 경우 분석 Average-case analysis Θ
4) 최선의 경우 분석 Best-case analysis Ω
◆ 복잡도 함수 (complexity function)
알고리즘의 복잡도를 나타내는 함수로, 음이 아닌 정수(input)가 주어지면 음이 아닌 실수(output)를 내어준다.
(단위 연산 횟수나 수행 시간은 음이 아닐 수밖에 없음)
복잡도 함수는 높은 차수항이 궁극적으로 그 성질을 좌우한다!!
ㆍ 대표적인 복잡도 함수


△ 아래로 갈수록 복잡도가 증가함
◆ Big-O 표기법 -최악의 경우
점근적 상한 (asymptotic upper bound) 으로 표기
점근적 상한 [정의] 주어진 복잡도 함수 f(n)에 대해서 g(n) ∈ O(f(n)) 이면,
n ≥ N인 모든 정수 n에 대해서 0 ≤ g(n) ≤ c×f(n)이 성립하는 양의 실수 c와 음이 아닌 정수 N이 존재한다.
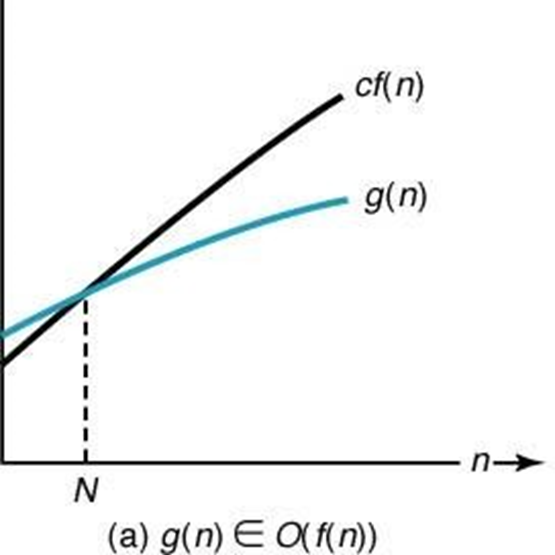
음이 아닌 정수 n이 무한으로 다가갈 때 언젠가는 f(n)이 g(n)보다 영원히 커지면,
cf(n)이 g(n)의 점근적으로 상한이라고 말한다. (c는 양의 실수)
또 g(n)은 O(f(n))에 속한다고 말한다
그 함수 g(n)은 cf(n)보다 궁극적으로 좋다고 말할 수 있다. (g(n)은 최소한 cf(n)보다는 빠르다~)
◆ small-o 표기법
복잡도 함수끼리의 관계를 나타내기 위한 표기법
-> Big-O 보다 멀리 있는 상한을 나타낸다고 보면 됨!

→ f(n)보다 더 낮은 최고 차수를 가진 함수들이 f(n)의 Small-o라고 볼 수 있음
g(n)이 o(f(n))에 속한다면,
g(n)이 궁극적으로 cf(n)보다 훨씬 좋다는 뜻!
※ Big-O와 Small-o의 차이점
|
◆ Ω 표기법 -최선의 경우
점근적 하한 (asymptotic lower bound) 으로 표기
점근적 하한 [정의] 주어진 복잡도 함수 f(n)에 대해서 g(n) ∈ Ω(f(n)) 이면,
n ≥ N인 모든 정수 n에 대해서 g(n) ≥ c×f(n) ≥ 0 이 성립하는 양의 실수 c와 음이 아닌 정수 N이 존재한다.
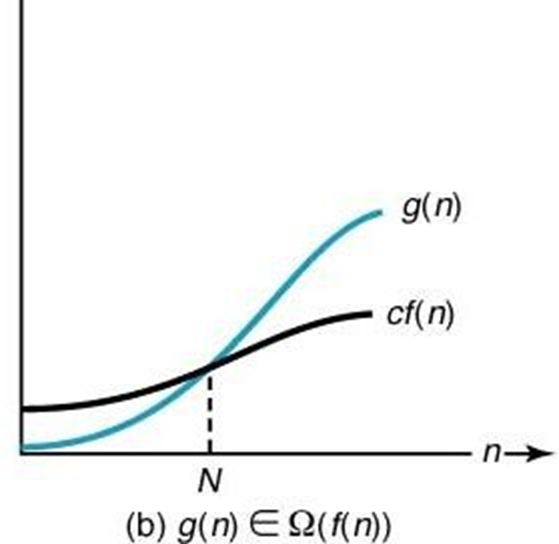
음이 아닌 정수 n이 무한으로 다가갈 때 언젠가는 f(n)이 g(n)보다 영원히 작아지면,
cf(n)이 g(n)의 점근적으로 하한이라고 말한다. (c는 양의 실수)
또 g(n)은 Ω(f(n))에 속한다고 말한다
그 함수 g(n)은 cf(n)보다 궁극적으로 나쁘다고 말할 수 있다. (g(n)은 아무리 빨라도 cf(n)보다는 느리다..)
◆ small-ω 표기법
복잡도 함수끼리의 관계를 나타내기 위한 표기법
-> Ω 보다 멀리 있는 하한을 나타낸다고 보면 됨!
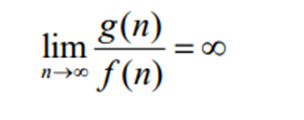
→ f(n)보다 더 높은 최고 차수를 가진 함수들이 f(n)의 Small 오메가 라고 볼 수 있음
g(n)이 ω(f(n))에 속한다면,
g(n)이 궁극적으로 cf(n)보다 훨씬 안좋다는 뜻!
◆ Θ 표기법 -평균의 경우
점근적 상한과 점근적 하한의 교집합 으로 표기

g(n)이 궁극적으로(점근적으로) Big-O(상한)과 Ω(하한)의 사이에 있는 것을 의미함
쉽게 말하면 평균적인 복잡도의 느낌!
이 경우, g(n)은 f(n)의 차수(order) 라고 한다.
◆ 알고리즘 복잡도와 컴퓨터의 능력
<문제풀이>
| Q1. 알고리즘의 복잡도가 cn일 때, t시간동안 문제 크기 m개의 문제를 해결한다고 하자. 기계의 처리 속도가 2배가 된다면 t시간동안 몇 개의 문제를 해결할 수 있는가? |
기계의 처리 속도가 2배가 됐을 때 t시간동안 해결할 수 있는 문제의 개수를 m+x개라 하자.
c(m+x) = 2cm
x =m
∴ 2m개의 문제를 해결할 수 있다.
| Q2. 알고리즘의 복잡도가 cn²일 때, t시간동안 문제 크기 m개의 문제를 해결한다고 하자. 기계의 처리 속도가 4배가 된다면 t시간동안 몇 개의 문제를 해결할 수 있는가? |
c(m+x)² = 4cm²
x = m
∴ 2m
| Q3. 알고리즘의 복잡도가 c2ⁿ일 때, t시간동안 문제 크기 m개의 문제를 해결한다고 하자. 기계의 처리 속도가 100배가 된다면 t시간동안 몇 개의 문제를 해결할 수 있는가? |
c2^(m+x) = c*100*2^(m)
x = lg100 = 6.~~
∴ m + 6
'CS > 알고릴라' 카테고리의 다른 글
| 5장. 되추적 (Back-tracking) (0) | 2023.05.16 |
|---|---|
| 4장. 탐욕적인 접근방법(Greedy Algorithm) (2) (0) | 2023.05.01 |
| 4장. 탐욕적인 접근방법 (Greedy Algorithm) (1) (0) | 2023.04.17 |
| 3장. 동적 계획법 (Dynamic Programming) (1) | 2023.04.13 |
| 2장. 분할 정복법 (Divide & Conquer) (0) | 2023.04.11 |




