센로그
1. Introduction to Inverse Kinematics 본문
IK란 뭐고, 왜 배우는지에 대한 내용.
◆ 관절체가 있는 캐릭터의 Animation

관절체가 있는 캐릭터 애니메이션이 현실적으로 느껴지게 하려면 몇가지 제한(constraint)이 필요함
1) 관절이 돌아갈 수 있는 최대 각도가 있음
2) 관절들은 서로 겹칠 수 없음
3) 관절 길이, 키 등 개인적 차이에 따라 물리적으로 타당하게 움직여야 함
◆ Inverse Kineatics (IK) 란?
관절체의 끝단(end-effector)의 움직임을 이용해 나머지 관절체의 움직임(position, rotation 등)을 결정하는 기술
모든 관절에 대해 각각의 움직임을 정의해줘야하는 Forward Kinematics (FK) 와 반대(Inverse)되는 기술!
◆ IK problem
IK문제는 비선형적(non-linear)인 계산을 풀어야 해서 복잡함
=> 비선형적인 계산을 근사해서 local minimum을 찾는 방식을 사용하도록 함!
*local minimum : 하나의 가장 좋은 답안(global minimum)을 찾기 힘들기 때문에, 대충 그럴듯해 보이게 풀어놓은 해
따라서 IK 문제의 해를 찾기 위한 몇가지 방법들이 있다.
- Jacobian Transpose
- Damped Least Squares (DLS)
- Damped Least Squares with Singular Value Decomposition (SVD-DLS)
.. 등등. 지금부터 이런 애들을 하나하나 공부해볼 것이다.
◇ IK problem - Jacobian 기반 접근 방법
"내가 관찰하는 시점에서만 가장 알맞은 것을(근사해서) 찾겠어..!!” 하는 방법
Jacobian을 사용해 비선형식들을 풀 수 있는 방법이 생김!
※ Jacobian이란?
복잡한 비선형식(non-linear)을 미분을 통해 선형 근사(linear approximation)시킴으로써,
선형 근사식으로 만들어주는 것을 의미함.
f1을 x로 편미분하고, y로 편미분하고,
f2를 x로 편미분하고, y로 편미분하고…
이렇게 만들어진 게 Jacobian matrix.
but, Jacobian 기반 접근방법은 다음과 같은 2가지 문제점이 있다.
1) Complex matrix - 복잡한 행렬 계산이 필요해서 속도가 느림. (비싼 연산)
2) Singularity problem - Jacobian이 풀리지 않는 경우가 있음
Jacobian 해를 구할 때는 Jacobian의 역행렬의 형태로 구함.
그러나 역행렬을 구한다는건 복잡한 과정이고, 존재하지 않을 수도 있음. (det(J)=0이면 역행렬 존재X)
ex) 내가 앞에 있는 물체를 잡기위해 손을 뻗었는데, 실제로 닿지 못하는 거리라 하자.
그런데 만약, “닿을 수 있으면서"와 같은 constraint를 걸어놓은 경우라면 실제로 못 닿으니까 해가 없는 것.
◇ IK problem - Newton method 기반 접근 방법
constraint가 없는 상황에서, 비선형 최적화 문제를 푸는 방법
IK문제를 최적화 문제의 형태로 접근함.
Jacobian 기반 접근방법의 문제점에 대한 대안 방법으로 역행렬 계산 없이 IK를 풀고자 하는 방법이 나왔음. (《Inverse kinematic without matrix inversion》, 2008). feedback loop를 통해 반복적으로 iteration 돌아서 접근하며 푸는 방법.
이 방법으로 Singularity problem은 해결했다. 그러나 얘도 여전히 느렸음..
그래서 나온 것이 Newton method 기반 접근 방법.
Newton method란, unconstrained한 상황에서 비선형 최적화 문제(non-linear optimization problem)를 푸는 방법임.
물론 IK에는 constraint가 존재하니까 이를 조금 변형해서 풀게됨
- 그 예시로, BFGS method <-나름 빠르고 핫함
요새 젤 마니 쓰이는 건 FABRIK’s Method. 게임쪽에서는 FABRIK을 많이 씀(https://grace7040.tistory.com/97)
또는 모션 캡쳐나 딥러닝으로 IK를 푸는 것도 많이 연구되고 있음.
◆ 관절체 모델(Skeletal structure)의 구조
관절체를 쓰려면, 관절체에 대한 올바른 규격(미리 처리된 motion data)이 있어야 하고
이에 따라 데이터를 로딩해야함 (올바른 계층적 연결과 constraint 만족 여부를 확인하기 위해서)
실제 우리 몸은 rigid가 아니지만 일단 rigid라 가정하고 모델링함.
<기본 개념>
- joint (관절). joint 를 구분하기 위해 'i번째 joint' 같은 형식으로 표현함
- link(bone) (뼈) : joint와 joint를 연결하는 것
- root : 관절체의 기준, 중심의 느낌. 보통 pelvis를 얘기함
- DOF (Degree Of Freedom) : 관절의 자유도
몇 개의 축에 대해 움직이냐에 관한 것.
예를들어, 양 옆으로 회전하는 것 밖에 안되면 DoF = 1이고, 2차원 평면으로 회전이 가능하면 DoF = 2
x, y, z축에 대해 회전과 이동이 모두 가능하다면 DoF = 6
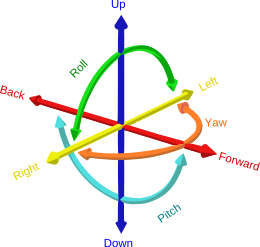
< parent-child system >

모든 joint들은 하나 이상의 parent와 n개의 child를 가짐. parent joint가 움직임에 따라 child joint도 움직임.
- chain : 부모(상위 joint)가 움직이면 자식도 움직이는 그런 애들의 그룹. IK에서는 chain 위주로 변화가 일어남.
- end-effector : 끝단
bone(또는 joint) 중에서 children이 없는 경우를 end-effector라고 함 (손끝, 발끝 등)
◆ Forward Kinemarics vs Inverse Kinematics
ㆍForward Kinematics
매 프레임마다 관절체들 각각의 회전과 위치를 정의해줘야 하는 것
Input: joint angles
Output: link positions and orientations, end effector position
- IK에 비해 퀄리티가 높음
- 만들기 어렵고 시간이 오래 걸림
- 유니크한 솔루션이 존재함
ㆍInverse Kinematics
input으로 end-effector들의 위치를 넣으면 나머지의 위치들이 알아서 만들어짐(chain 위주로 변화)
Input: end effector position
Output: joint angle
- FK에 비해 퀄리티가 떨어짐
- 만들기 쉽고 금방 만듦
- best 솔루션을 찾는 것. (항상 하나의 솔루션만 있는 것은 아님)
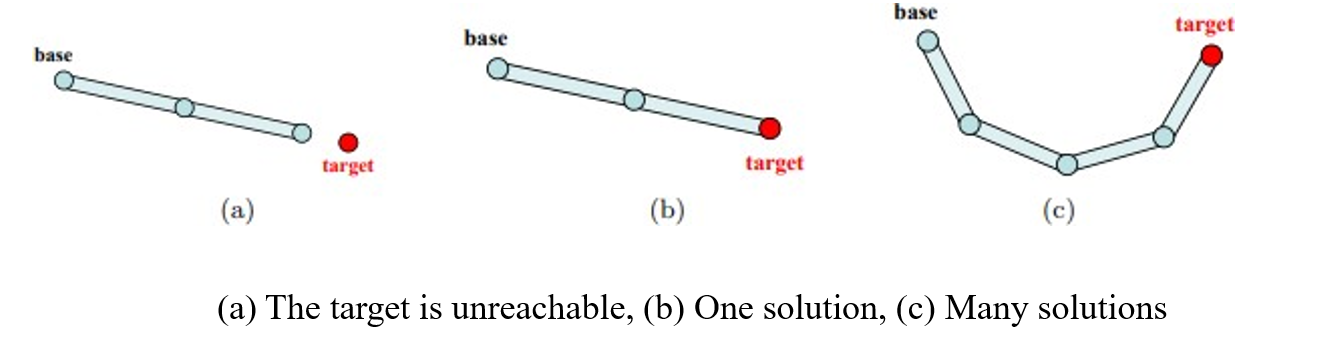
c인 경우, 다양한 형태의 해가 나올 수 있기 때문에 그중에서 어떤 해를 선택해야 하느냐가 어려움ㅇㅇ
◆ Geometric Algebra
IK에서, 3차원상 축 회전을 편리하게 표현하기 위해 Geometric Algebra(기하 대수)를 사용함.
대부분의 IK는 object orientation과 rotation을 사용해서 구현된다.
그렇다면 3차원상에서 물체의 rotation을 쉽게 표현할 방법은 없을까?
→ 3차원상에서 축 회전을 편리하게 표현하기 위해 Geometric Algebra를 사용함.
Geometric Algebra에서는 3차원에서 orientation과 rotation을 편리하게 표현하기 위한 object를 제공함
→ Rotor. 원점에 대한 회전을 표현하는 객체
◇ Geometric Algebra - Bivector (이중 벡터)
방향성을 가진 평면

ㆍScalar : 방향성을 갖지 않는 특정값 (0-dimensional)
ㆍVector : 방향을 가진 값 (1-dimensional)
ㆍBivector : 방향(CW, CCW)을 가진 평면 (2-dimensional)

두 벡터가 크기와 방향이 같다면 같은 벡터인 것처럼,
두 Bivector가 넓이와 방향이 같다면 같은 Bivector이다.

단, 두 Bivector의 넓이가 같더라도 방향이 다르면 다른 Bivector임!
암튼 핵심은 뭐냐면,
두 Bivector을 더하면 새로운 (방향이 좀 바뀐) Bivector가 튀어나온다는 것!

A + B = C
※ 기저 Bivector들의 합으로 Bivector을 표현할 수도 있음
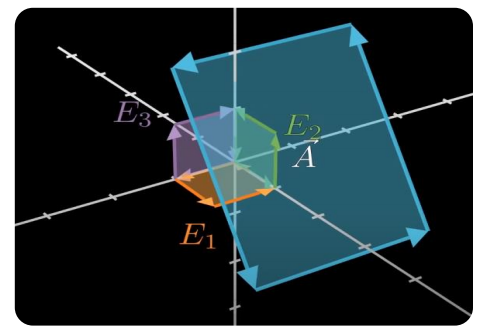
E₁, E₂, E₃가 기저일때, A = aE₁ + bE₂ + cE₃ 이런 식으로 나타낼 수 있다는 뜻. (a, b, c는 상수)
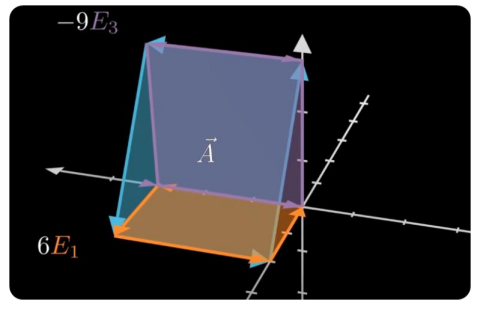
A = 6E₁ - 9E₃이런 식!
이는 좌표 형식으로도 표현 가능. (6, 0, -9)
◇ Geometric Algebra - Inner Product
Inner Product(내적)은 정사영 벡터의 크기
벡터 u와 벡터 v의 내적은 uㆍv 또는 < u, v >로 표기함.

내적의 결과값은 스칼라 값임.
따라서, 내적 연산의 결과값만 갖고는 다음 그림에서 원래 벡터가 뭔지에 대한 정보를 알 수 없음.

Inner product uㆍv = ||u||||v||cosθ
유 닷 브이
uㆍu = 1
uㆍv = vㆍu
| * cos(θ) = cos(-θ)이므로 방향 구분이 어려움 |
◇ Geometric Algebra - Outer Product
!= cross product
Outer Product(외적)의 크기는 평행사변형의 넓이
3차원 공간에서, 벡터 u와 벡터 v의 외적은 u Λ v 로 표기함.
외적의 결과로 bivector가 만들어짐!
Cross product u Λ v = ||u||||v||sinθ
유 웻지 브이
u Λ u = 0
기하학적으로는, 두 벡터가 평행하면 sinθ = 0이라 평면이 만들어지지 않기 때문!

u Λ v의 결과 bivector의 방향은 u의 방향에 따라 결정됨. (u의 방향대로 CW/CCW로 돌음)

u Λ v = - v Λ u ← anti-commutative. 교환법칙 성립 안함!!

(u Λ w) + (v Λ w) = (u + v) Λ w
| * sin(θ) != sin(-θ)이므로 +,-의 방향 구분이 가능해짐! 그러나 θ가 90도 넘어가면 마찬가지로 구분 못 하는 이슈.. -> 그래서 등장한 게 Geometric product |
※ Outer product의 수학적 설명!
Cartesian sapce에서 기저 e1, e2는 다음과 같이 정의됨. (x, y)
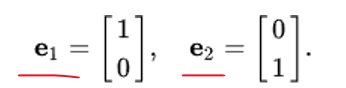
이때 벡터 v, w를 다음과 같이 정의해보자.
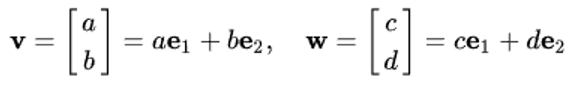
v와 w는 유니크한 평행사변형(parallelogram)을 이룸.
평행사변형의 넓이는 다음과 같이 | det [ v w ] |로 표현할 수 있음.
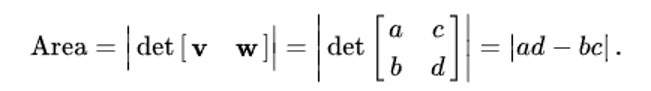
따라서 v Λ w는 다음과 같이 표현할 수 있음!
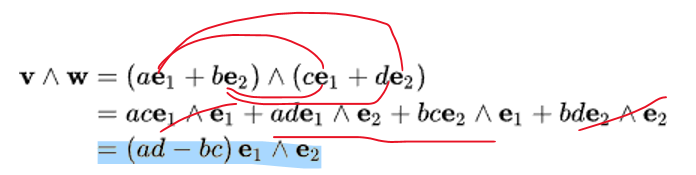
(자기자신의 웻지는 0이니까 날린 거 ㅇㅇ)
기저들의 웻지에다 스칼라가 곱해진 느낌.
같은 맥락에서, 3차원을 보자. (e₁, e₂, e₃)이 기저일 때, u와 v의 웻지는 다음과 같음
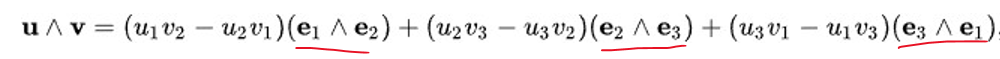
근데 이 형태에서 알 수 있는 게 있음.
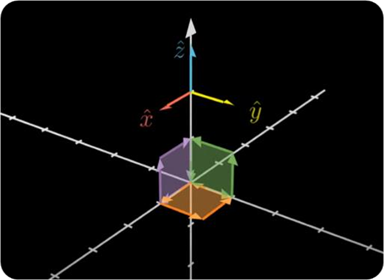
만약, Bivector e₁ Λ e₂, e₂ Λ e₃, e₃ Λ e₁를 기저로 사용하면, 간편하게 (a, b, c) 형태로 표현할 수 있겠구나! 라는 것.
즉, bivector 평면 자체를 기저로 사용할 수도 있다는 점.
그렇게되면 각각의 기저 bivector에 상수를 곱하는 형태로 표현 가능하므로, 좌표 형식으로 표현 가능 ㅇㅇ
◇ Geometric Algebra - Geometric Product
cos과 sin을 합쳐서 표현하면 어느 방향에서 왔는지 확실히 알 수 있음!
Geometric product uv = uㆍv + u Λ v
< 특징 >
1) uu
θ = 0일때, cos0 =1 이고 sin0 = 0이므로 uu = uㆍu = ||u||² 만 남음

2) u inverse

3) uw와 wu
내적은 commutative하고, 외적은 anti-commutative하기 때문

이므로, 다음과 같이 표현 가능.

4) basis 표현
두 직교기저벡터 사이의 θ = 90이므로, Geometric product는 Outer product와 같음
cos90 =0 이고 sin90 = 1이고, 기저벡터의 경우 unit 벡터(크기 1)이기 때문임.
따라서 다음과 같이 새롭게 기저를 표현 가능.

또 이 경우에, x∧y = -y∧x이므로 xy = -yx 이다.
◇ Geometric Algebra - Geometric Product representation
pseudoscalar i를 이용해 복소수 범위에서 표현하는 방법
앞서 Geometric product uv의 정의가 다음과 같다고 했었다.
Geometric product uv = uㆍv + u Λ v
그러나, 스칼라 값과 벡터 값을 합칠 수는 없자나?
그래서 등장한 것이 i(허수)를 이용해 복소수 범위에서 표현하는 방법임
a + bi = scalar + bivector(imaginary)
2차원 기저가 {x, y} = {(1,0), (0,1)}라 하자.
선형대수에서 2차원 벡터 u = ax + by로 표현가능. 2개의 항.

기하대수에서 2차원 V = a + bx + cy + dxy라는 multi vector로 표현됨. 4개의 항.

따라서, 가장 고차원인 xy라는 기저를 pseudoscalar로 치환해서 표현하자! 하는 것임.
pseudoscalar란, 마치 스칼라처럼 동작하는 양을 의미함.
기저 벡터가 {x,y}이면 pseudoscalar는 xy.
마치 허수처럼 작동함. (xy)² = -1


x = {1,0}, y = {0,1} 이므로, xx = yy = 1 (||x||² = 1, ||y||² = 1)이다.
ui의 경우, 2xi + yi = 2xxy + yxy = 2xxy - xyy = 2y - x
ui 처럼, Pseudoscalar을 뒤에 곱하면 반시계 방향(CCW)으로 90도,
iu 처럼, Pseudoscalar를 앞에 곱하면 시계 방향(CW)으로 90도 회전함.
◆ 2D Rotation with Geometric Algebra
근데 우리가 알고싶은 건, 90도 회전이 아니라 θ만큼의 회전임.
그럼, Geometric Algebra로 2차원 회전을 어떻게 표현하는지 보자!
우리는 두 방법으로 회전을 표현할거야.
ㆍ1. 어떤 각 θ 만큼의 회전
ㆍ2. u에서 v만큼의 회전
회전을 표현하기 위해서 복소수를 사용하면, 쉽게 결과를 찾을 수 있을거야! 라는 아이디어.
1) Euler's formula - 어떤 각 θ 만큼의 회전
극좌표에서 r의 θ만큼 회전을 rθ라고 하듯이, 우리도 회전각을 저런식으로 표현할 수 있을 거 같아.
벡터 u를 θ만큼 회전시키고 싶을 때, u(cosθ + isinθ) 와 같이 쓸 수 있을 것임.
이때 Euler의 공식에 따라, cosθ + isinθ는 e^(iθ)로 표현할 수 있다.
따라서 ue^(iθ)와 같이 회전을 표현할 수 있음!


이 θ에다가 내가 회전시키고 싶은 값 넣어주면 그만큼 회전할 것.
2) Conjugate - u부터 v까지 이동했다는 정보를 알고 있을 때 회전

만약 u와 v가 단위벡터이면, uv = e^(iθ)
uv = uㆍv + u∧v 이고,
vu = vㆍu + v∧u = uㆍv - u∧v이므로, uv의 켤레인 (uv)* = vu라 할 수 있다.

그림 과같이 w를 u에서 v만큼 회전시키고 싶다면, wuv (=(uv)*w = vuw)와 같이 표현하면 됨

◆ 3D Rotation with Geometric Algebra
우리가 진짜 해야할 건 3차원상에서의 회전!
3차원 멀티 벡터를 표현하려면 원래 8개의 항이 필요함.
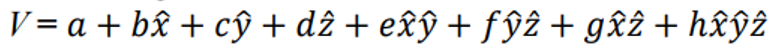
멀티 벡터 V에 i(=xyz)를 곱해서 회전을 표현해주자.
i를 곱하고, 곱해서 1이 되는 애들을 줄여서 묶으면 다음과 같이 4개 형식으로 표현 가능
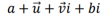
이렇게~
일단.. 2차원상에서 했던 것처럼 한번 해보자.

3차원에서, v = 3x + 2y + z일 때
v를 z축 기준 90도 돌리는 경우를 생각해보자~
이 결과로는 3y - 2x + z가 나와야 함.
우선, xy라는 bivector을 가지고 돌리면
vxy = (3x + 2y + z)xy = 3y - 2x +xyz가 나옴. xyz라는 trivector가 너무 드러움 ㅠㅠ
그럼 다른 방법을 써보자.
vxy = (xy)*v = yxv라 했었다.
yxv = yx(3x + 2y + z) = 3y - 2x - xyz이다.
오? 둘을 합치면 trivector을 없앨 수 있을 것 같은데?? 라는 아이디어.

yxvxy = yx(3x+2y+z)xy = 3yxxxy + 2yxyxy + yxzxy = -3x -2y + (xy)*yxz = -3x -2y + yxyxz = -3x -2y + z
trivector가 사라졌다!!!!!
근데, 앞뒤로 곱하다보니까 너무 많이 돌았네?
좋아. 그럼, 앞뒤로 곱하는 거니까 각도를 반씩만 넣어서 해보자.

축~ 정답~!!
3차원에서의 회전은, 앞에서도 반만큼, 뒤에서도 반만큼 옮겨주는 방식으로 해야하는구나!
즉 i평면을 기준으로 θ/2만큼 옮겨주는 방식으로 쓰게 된다.
이렇게!

이때

를 Rotor라고 부른다. 이것은 쿼터니언과 유사함.
◆ 3D Rotation with Geometric Algebra - Quaternion
3차원 공간상에서의 회전을 편리하게 나타낼 수 있도록 하는 체계. (쿼터니언은 3차원에서만 동작함!!!)

오일러 방식(왼쪽 그림)은 x,y,z 축 기준으로의 회전만 표현할 수 있음.
쿼터니언(오른쪽 그림)은 임의의 축을 기준으로 회전 표현 가능!
어떤 축을 기준으로 몇도 회전하는지 표현하는 것. (axis-angle 로 표현)

3차원에서, 고정된 포인트에 대한 모든 강체 회전은,
어떤 고정된 축(euler axis)을 기준으로 몇 도 회전하는지로 표현할 수 있다.
쿼터니언은 이런 회전을 4개의 숫자로 간단히 표현함.
(ω, x, y, z)의 형태.
u벡터 기준으로 θ만큼 회전을 생각해보자.

로 표현할 수 있다.
오일러 공식에 의해 다음과 같은 q를 정의해보자.

이제 p = (p_x, p_y, p_z)를 돌려보자. 앞서 Rotor에서의 개념을 갖고오면, 다음과 같이 회전 상태를 표현할 수 있따!


굿.
추가로, 이 과정을 다음과 같은 Rotation Matrix 형태로 만들 수도 있음.

쿼터니언 ↔ Matrix 변환 가능하다는 뜻~ matrix로 연산하면 빠르니까!
(관련 내용 : https://grace7040.tistory.com/93)
'게임 > Inverse Kinematics' 카테고리의 다른 글
| 6. Heuristic Inverse Kinematics Algorithms (0) | 2023.05.30 |
|---|---|
| 5. Quasi-Newton Method for Inverse Kinematics (0) | 2023.05.29 |
| 4. Newton Method for Inverse Kinematics (0) | 2023.05.29 |
| 3. Jacobian Inverse Methods for Inverse Kinematics (0) | 2023.05.27 |
| 2. Numerical Solution of Inverse Kinematics (0) | 2023.04.25 |





