센로그
4. Newton Method for Inverse Kinematics 본문
◆ Newton Method for IK
Newton method는 IK 문제와 같은 비선형 방정식을 풀기위해 (자코비안과는 다르게) 반복적으로 접근하는 방법이다.
< Newton Update Functions >
| root finding | optimization | |
| 단변수 (uni-variate) |  |
 |
| 다변수 (multi-variate) |  |
 |
< 전체적인 오버뷰 >
ㆍ문제 정의 :
IK 문제는 joint angle 등의 변수를 모르는 비선형 연립 방정식의 형태이다.
우리는 end effector가 최대한 target position에 가까이 가도록 하는 연립방정식의 해를 구해야 한다!
ㆍ뉴턴 방법 특징 :
Newton method는 비선형적인 문제를 선형적으로 접근한다.(Problem linearization)
매 step마다 조금씩 접근하면서 joint angle 등의 변수를 업데이트해 나가며 반복한다. (Iterative update)
반복하면서 어느정도 충분히 다가갔을 때(수렴), 컷 하는 기준이 있다. (Convergence check)
이런 방식으로 접근해서 푸는 방법들을 Newton family라고 부름.
Newton family는 보통 2차 테일러 급수를 활용해 풀게 된다. (f(x)의 2차 테일러 급수의 확장)

어떤 f(x)를 σ만큼 이동시킨 f(x+σ)는, f(x) + transpose(gradient f(x))σ + (1/2)transpose(σ)Hessian(f(x))σ와 같다.
Hf(x)는 f(x)의 헤시안 행렬을 의미한다.
헤시안은 편미분 두번 때려서 만들어지는 친구였는데, 이 친구는 엄청 많은 비용을 필요로 한다. 리얼 타임이 불가할 것임.. 이런 계산 복잡도를 줄이기 위해서 헤시안을 구하는 대신, gradient를 기반으로 헤시안의 근사를 구하는 방법(ex: BFGS)도 있따.
IK를 푸는 Newton method는 두 가지 방법이 있다.
- root finding
=> 1차 미분만 함 => 자코비안만 필요 - optimization (find minima or maxima)
=> 2차원 => 자코비안, 헤시안 필요
◆ Newton Methods vs Jacobian-based Method
ㆍNewton method의 장점:
- Fast convergence: 수렴이 빠름. 초기 추측이 잘 들어맞을 경우, 자코비안 방법에 비해 훨씬 더 빨리 수렴에 도달함
- Quadratic convergence: 특정 조건에서, quadratic convergence(2차 수렴)를 제공함 => 에러가 엄청 빠르게 감소함.
- Applicability to nonlinear problem: IK같은 비선형 문제에 대한 해를 잘 찾아낼 수 있음. 자코비안 방법은 해가 안 풀릴 경우가 있는데 반해, 뉴턴 메소드는 안정적으로 이상적인 해를 찾아갈 수 있다
ㆍNewton method의 단점:
- Sensitivity to initial conditions: 초기 추측을 제대로 못하면 헤멤. 초기 추정치가 실제 해에서 멀리 떨어져 있는 경우, 방법은 수렴하지 않거나 원하지 않는 local minimum에 수렴할 수도 있음
- Computation of Jacobian and Hessian: 자코비안 및 때로는 헤시안을 구해야 해서 계산 비용이 큼
- Inverse of Jacobian: 일부 경우에서는, 자코비안의 역행렬를 써야할 수도 있음..
◆ Taylor Series
함수가 무한대로 미분 가능(infinitely differentiable)하다면, Taylor series라는 power series(멱급수; 거듭제곱 급수)로 만들 수 있다.
※ Power Series
n이 0부터 시작해서 무한대로 갈때, 다음과 같은 형태를 파워 시리즈라 함.
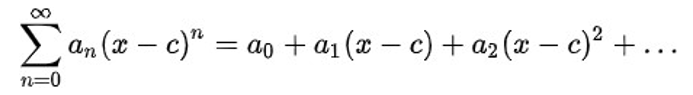
an는 n번째 계수(coefficient)를 나타내고, c는 상수.
파워 시리즈의 특수 형태가 테일러 시리즈이다.
모든 함수는 다른 함수들의 합으로 표현할 수 있고,
모든 곡선은 다른 어떤 곡선들의 합으로 표현할 수 있다.
f(x)가 끊임없이 미분할 수 있다면, 다음과 같은 x = a에서의 테일러 급수를 만들 수 있다.
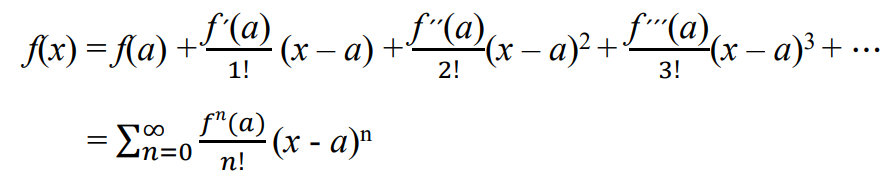
기하학적 의미를 살펴보자면,
어떤 곡선의 1차미분 + 2차미분 + 3차미분 +…을 더해주면 결국 원래 곡선이 된다. 라는 것.
보통 3차 이상은 의미없다고 생각해서 안보는 경우가 많다.
a = 0일 때 테일러 급수를 Maclaurin 급수라고 함.

◆ Newton-Raphson Method and IK
root finding
초기 좌표에서 미분하고 기울기 연장해서 x절편 찾고, 거기서 다시 미분하고 기울기 연장해서 x절편 찾고...
0이 되거나, 어느정도 0에 가까워 지면 종료
Newton Raphson method는 어떤 비선형함수의 root를 찾는 문제임.
(root-finding; 함수값을 0으로 만드는 x값을 찾는 문제)
IK 문제는 다음 식을 만족하는 joint angle θ를 찾는 문제였다.
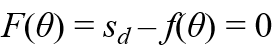
( f(θ) = sd ←이건 FK에서 쓰던 식임! θ 넣으면 end effector position 나오는 식.)
이 문제의 해가 θd라 하자. 이제 여기에 Newton-Raphson method를 써보자!

이 그래프에서, F(θ) = 0으로 만드는 θd를 찾아야 한다.
초기 추측을 θ0이라 하자. 우리는 F(θ0) = sd - f(θ0)를 계산할 수 있다.
계산 결과로 얻은 (θ0, F(θ0))지점에서 미분을 때리면 기울기가 나옴.
이 기울기를 쭉 연장한 직선의 x절편을 θ1이라고 하자.
다음 식이 나온다.

θ1을 구하기 위해, θ1 - θ0 = Δθ를 보자.

이로부터 θn+1에 관한 일반화된 식이 도출될 수 있다.

이제 다시 F(θ1)로 계산해보자!... 이런식으로 쭉 하다보면 F(θ)가 점차 0으로 수렴하게 될 것이다.
반복할수록, θn+1이 θd를 향해 갈 것이다. 충분히 수렴했다고 판정했을 때 그만풀면 됨!
=> sd - f(θ)에 θn을 넣었을 때 얼마나 0에 가까운지 확인해서, 어느정도 조건 내로 수렴했으면 그만두면 됨.
이때, sd - f(θn) = F(θn)이고, f`(θn) = -F`(θn)이므로 다음과 같이 나타낼 수 있다.

◆ Newton Method and Optimization Problem
optimization
F(θ)를 2차 테일러급수 로 바꾸고, 양변을 Δθ로 미분해서 F`(θ) = 0 (변곡점)이 되도록 하는 Δθ를 찾는다.
초기 추측값 θ0부터 시작해서 Δθ만큼 더했을 때 F를 최소화하는 Δθ를 찾아나감.
그러나 사실! sd - f(θd)를 0으로 만드는 θd를 찾는 문제는 실용적이지 않다..
그래서 이번에는! sd - f(θd) 를 최소화하는 문제로 바꿔보자! (반드시 0이 아닐 수도 있음)
원래 root finding으로 풀던 문제를 optimization으로 풀어보자는 뜻.
root finding은 목적 함수를 0으로 만드는 근을 찾는 문제이고
optimization은 목적 함수를 최솟값으로 만드는 근을 찾는 문제. 이때 최솟값은 반드시 0이 아닐 수도 있음
F(θ)를 테일러 급수로 바꿔보자.
θ0은 초기 추측값이고, Δθ는 θ를 얼마나 움직일지를 나타낸다고 할 때 다음과 같이 표현할 수 있다. (Δθ = θ - θ0)
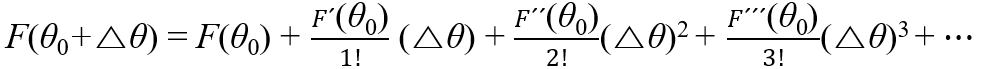
우리는, 초기 추측값 θ0부터 시작해서 Δθ만큼 더했을 때 F를 최소화하는 Δθ를 찾고 싶다.
이말은 즉슨, (θ0 + Δθ, F(θ0 + Δθ))가 변곡점(stationary point)에 도달한다는 것을 의미한다.

변곡점은 1차 미분때렸을 때 0이 되는 지점(F`(θ) = 0)으로
이 지점은 local minima, local maxima, saddle point 셋 중 하나가 될 수 있다.

우선 테일러 급수의 2차부터는 잘라내자.
그러고나서, 양변을 Δθ로 미분해서 F`(θ) = 0으로 놓고 문제를 풀어보자.
그러면 Δθ를 찾을 수 있다. (θ0 + Δθ가 변곡점으로 도달하도록 하는 Δθ를 의미한다.)
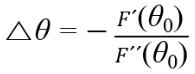
아까는 1차원 접선을 그어가면서 수렴해갔는데, 이번에는 2차원 함수를 사용해 접근하는 것임.
== 2차 수렴. 1차 수렴보다 속도가 훨 빠름!!

2차 함수의 최소값 위치를 기준으로 θn+1을 업데이트해나감.
1) root finding
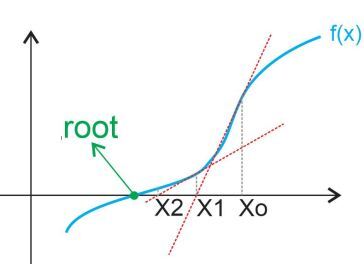
2) optimization
◆ Multivariate Newton Method - root finding
Jacobian을 사용하는 vector valued function
앞에서는 미지수 θ가 하나만 있었는데, 사실 IK는 여러 θ들이 관여함. 다차원, 다방정식이 들어감. Multi variate.
어깨 움직이면 팔도 움직이고 손도 움직이자나. 최종 위치에 관여하는 function들이 참 많음
관절 각자의 θ를 결정해줘야 하기 때문.
따라서, 다음과 같은 θ 벡터를 변수로 가지는 vector-valued function F(θ)를 정의한다.

F(θ) = sd - f(θd)는, FK를 통해 결정된 desired end effector pose와 현재 end effector pose 사이의 차이를 나타낸다.
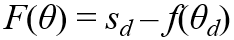
n개의 변수에 대해 n개의 연립 방정식을 풀 것이다.

root finding을 통해서, F(θ)를 벡터값 함수로써 풀자.
이에 따라 미분도 n개로 확장되어야 하기 때문에, Jacobian이 등장함.
θn이 현재 추측이고, θn+1이 다음 추측이라 하자.

단변수일 때는 1차 미분으로 풀었는데, 이젠 Jacobian으로 푼다! 라는 것.
(O(Δθ²)은 차수가 높은 부분들로, 근사할 때 무시될 수 있는 부분을 의미함)

J(θn)은 그림의 θn에서 추정한 F의 Jacobian matrix를 의미한다.
root finding 문제는 F(θn+1) = 0이 되는 θn+1을 찾는 문제이다. 그러므로 우리는, 다음과 같이 방정식을 다시 쓸 수 있다.

이로부터 다음 식을 도출할 수 있다.

실제 예시를 보자!
어떤 로보틱 시스템이 있다고 하자.
이 로보틱 시스템은 4개의 end effector와 8개의 joint가 있다.
얘들이 각각 3차원 dimension의해 정의 된다 하자. (x, y, z)
그러면 F(θ)는 12차원 벡터로 정의될 것임! (3차원 * 4개의 end-effector)
그러면 J(θ)는 12x8 행렬. F(θ)에 대한 8개 joint들의 1차 편미분을 포함한.
θ0~θn까지 반복문 돌면서 업데이트하다가, 종료조건 도달하면 종료.
◆ Multivariate Newton Method - optimization
에러들의 제곱 합을 최소화하는 scalar valued function
gradient, hessian 사용
이번에는 optimization 측면에서 보자.
우리의 목표는, 스칼라값 objective function을 최소화하는 joint angle들을 찾는것이다.
이때 object function은 에러들의 제곱 합(각 end effector들의 sd - f(θ)의 제곱 합)을 나타낸다.
마찬가지로 sd는 FK를 통해 구한 desired end-effector pose를 의미함.



단변수일 때는 1차 미분으로 풀었는데, 이젠 Gradient로 푼다! (2차 미분은 이젠 Hessian으로)

양변을 미분하면, 다음과 같다
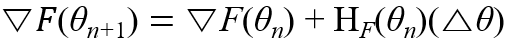
미분을 했는데 Gradient가 나오는 이유는, F가 multi variated scalar-valued function이라 했기 때문.
이런 애를 1차 미분하면 gradient가 나옴. 그리고 2차 미분하면 hessian이 나옴.

HF(θn)은 그림의 θn에서 추정한 F의 Hessian matrix를 의미한다.
optimization 문제는 ∇F(θn+1) = 0이 되는 θn+1을 찾는 문제이다. 그러므로 우리는, 다음과 같이 방정식을 다시 쓸 수 있다.

이로부터 다음 식을 도출할 수 있다.

실제 예시를 보자!
어떤 로보틱 시스템이 있다고 하자.
이 로보틱 시스템은 4개의 end effector와 8개의 joint가 있다.
얘들이 각각 3차원 dimension의해 정의 된다 하자. (x, y, z)
우리는 scalar valued object function F(θ)를 정의해야 한다.
e₁² + e₂² +e₃² + e₄² 꼴로 정의될 것임. (en은 end effector n 에서의 에러)
그러면 F(θ)는 12차원에 대한 에러 제곱 합으로 정의될 것임!
그러면 ∇F(θ)는 8차원 벡터로, F(θ)에 대한 8개 joint 각도의 1차 편미분을 포함함.
HF(θ)는 8x8 행렬. F(θ)에 대한 8개 joint들의 2차 편미분을 포함함.
θ0~θn까지 반복문 돌면서 업데이트하다가, 종료조건 도달하면 종료.
◆ 마무리
▶ IK 문제는 다변수 문제를 해결하는 것입니다.
따라서 단일 변수인 경우는 다변수 경우로 변환되어야 합니다.
=> 도함수 𝐹´(θn)대신에 그레디언트 ▽𝐹(θn)으로 대체되어야 합니다.
=> 2차 도함수의 역수(reciprocal)인 1/F``(θn) 대신에 헤시안 행렬의 역수인 1/HF(θ0)로 대체되어야 합니다.
=>2차 도함수의 역수는 함수의 곡률에 대한 정보를 제공합니다.
=> 2차 도함수가 너무 큰 경우, 역수는 거의 0에 가까워져 해당 지점에서 함수가 높은 곡률을 가지고 있음을 나타냅니다.
=> 2차 도함수가 0에 가까운 경우, 역수는 커져서 해당 지점에서 함수가 낮은 곡률을 가지고 있음을 나타냅니다.
'게임 > Inverse Kinematics' 카테고리의 다른 글
| 6. Heuristic Inverse Kinematics Algorithms (0) | 2023.05.30 |
|---|---|
| 5. Quasi-Newton Method for Inverse Kinematics (0) | 2023.05.29 |
| 3. Jacobian Inverse Methods for Inverse Kinematics (0) | 2023.05.27 |
| 2. Numerical Solution of Inverse Kinematics (0) | 2023.04.25 |
| 1. Introduction to Inverse Kinematics (0) | 2023.04.08 |




