센로그
3. Jacobian Inverse Methods for Inverse Kinematics 본문
◆ Singular Value Decomposition (SVD)
뒤에 나올 pseudo-inverse matrix의 개념을 이해하기 위해, SVD(특잇값 분해)의 개념부터 설명하고 넘어가겠음!
■ SVD Introduction
SVD(Singular Value Decomposition)는 고윳값 분해(Eigen Decomposition)과 극분해(Polar Decomposition)과 관련이 있음.
선형 대수에서, 행렬의 SVD는 해당 행렬을 세 개의 행렬로 factorization하는 과정입니다.
※ Matrix factorization(decomposition)이란?
Matrix factorization는 행렬을 여러 부분으로 분해하여 곱셈을 통해 원래의 행렬을 재구성하는 과정입니다.
이를 수행하는 여러 가지 방법이 있으며, LU 분해, Cholosky 분해, QR 분해 등이 있습니다.
우리는 행렬 A를 벡터 x와의 곱셈을 통해 새로운 벡터 Ax를 생성하는 '변환'으로 생각할 수 있습니다.
- [A]ij 또는 aij :행렬 A의 i번째 행과 j번째 열에 위치한 원소를 의미함
- 행렬 A가 벡터 x에 대해 일반적으로 가하는 효과는, rotation과 stretching의 조합임.
◆ Basic of Linear Algebra
뒤에 나올 개념들을 이해하기 위한, 기초 선형대수 복습 시간~
■ Transpose 전치



■ Partitioned Matrix 분할 행렬

일 때, B를 다음과 같이 u벡터들로 나눠서 표현할 수 있습니다.


이때 각각의 u벡터를 전치해서 B의 전치행렬을 표현할 수 있습니다.


■ Eigen Values & Eigen vectors 고유값 λ & 고유 벡터
Au = λu
벡터의 방향을 변경하지 않고 크기를 변경하는 유일한 방법은 스칼라와 벡터를 곱하는 것입니다.
만약 우리가 벡터 u와 스칼라 λ를 가지고 있다면, λu는 같은 방향을 가지고 크기만 다른 벡터입니다.
행렬 A의 고유벡터(eigen vector)는 Au = λu를 만족하는 영이 아닌 벡터 u로 정의됩니다.
여기서 λ는 A의 고유값(eigen value)이라고 불립니다.

여기서 u₁, u₂는 B의 eigen vector입니다. (Bu₁ = λ₁u₁, Bu₂ = λ₂u₂)
이때 대응하는 eigen value의 값은 각각 λ₁ = -1, λ₂= -2 입니다.
■ Eigen Decomposition of a matrix (AP = PD) 행렬의 고유값 분해
정사각 행렬 A를 고유값과 고유벡터로 분해해서 표현한 것. AP = PD. A = PDP⁻¹
정사각 행렬 A를 고유값과 고유벡터로 분해하는 것은 "행렬 대각화(matrix diagonalization)"의 일종이다.
이를 진행해 보겠습니다. A가 고유값 λ1, λ2, ..., λk와 이에 대응하는 선형 독립적인 고유벡터 X1, X2, ..., Xk를 가진다고 가정해 봅시다. 이는 다음과 같이 표현될 수 있습니다:

이로부터, 다음과 같이 eigen vector들의 행렬인 P와, 대각 성분으로 eigen value들을 갖고있는 행렬 D를 정의할 수 있습니다.

결과적으로, 다음과 같이 AP = PD가 됩니다.

양 변에 P⁻¹을 곱하면, A = PDP⁻¹ 형태가 됩니다.
이 분해는 항상 정사각 행렬 A에 대해 가능합니다.
방정식 양변을 제곱하면 다음과 같습니다:
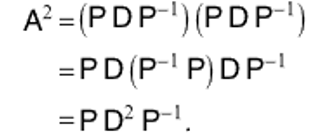
이것의 일반화된 형태는 다음과 같습니다.

이로부터 A inverse를 구할 수 있씁니다.
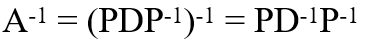
이때 D inverse는 다음과 같은 간단한 대각 행렬 형태입니다.
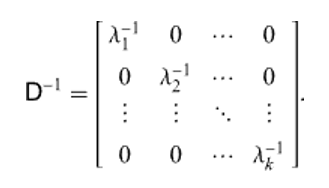
근데.. 고유값 분해는 제약이 있따! 정사각 행렬(nxn)에 대해서만 분해가 가능했음.
이걸 일반적으로 확장시킨 게 특이값 분해.
mxn 크기의 A에 대해, ATA와 AAT는 무조건 정사각 행렬이 된다는 아이디어.
■ Singular Value 특이값 σ
m×n 행렬 A에 대해, A의 특이값은 행렬 ATA 또는 AAT의 고유값의 양의 제곱근(root).
(ATA와 AAT의 고유값은 같음)
행렬의 특이값(Singular Value)은 행렬에 대한 유용한 정보를 제공할 수 있는 숫자들의 집합입니다.
유용한 정보란 행렬의 랭크(rank), pseudo inverse 등을 의미합니다.
주어진 m×n 행렬 A에 대해, A의 특이값은 행렬 ATA 또는 AAT의 고유값들의 양의 제곱근입니다.
특이값은 σ1, σ2, ..., σi와 같이 표기되며, 여기서 i는 A의 랭크(rank)를 나타냅니다.
Singular Value 찾기 예시)

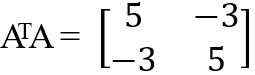
eigen value를 먼저 찾아주자.
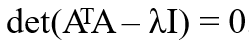
대각성분 원소에 각각 λ만큼 뺐을 때의 determinant = 0 을 계산해서, λ를 구할 수 있음.

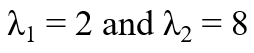
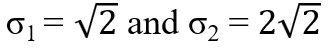
■ Rank 차수
A의 선형 독립(linearly independent)적인 열들의 최대 개수
선형 대수학에서, 행렬 A의 랭크(rank)는 그 열(column)들에 의해 생성된 벡터 공간의 차원을 나타냅니다.
이는 A의 선형 독립(linearly independent)적인 열들의 최대 개수와 같습니다. (다른 열들로 표현 불가능)
※ 선형 독립(linearly independent)
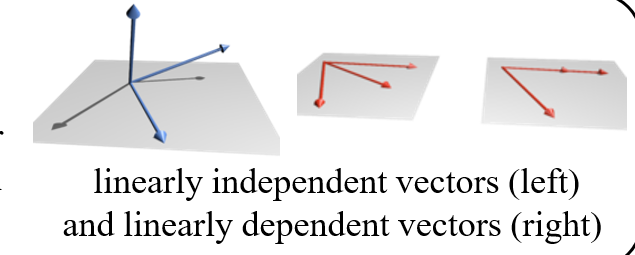
다른 벡터로 표현할 수 없는 경우.
만약 행렬의 랭크가 해당 차원에서 가능한 가장 큰 값과 같다면(모두 선형독립이라면), 그 행렬은 full rank를 가진다고 말합니다. 그렇지 않을 경우, 행렬은 rank-deficient라고 합니다.
※ row들이 선형 독립인지 체크하는 방법. => Row reduction
어떤 row로 나머지에다 빼고 더하고 ...하면서 최종적으로 행 사다리꼴(row echelon) 형태로 만들어 주자.
그러다가 0 0 0이 되면, 다른 벡터들로 그 벡터를 표현했다는 얘기이므로 선형독립이 아닌 놈임
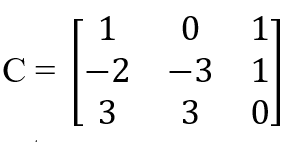
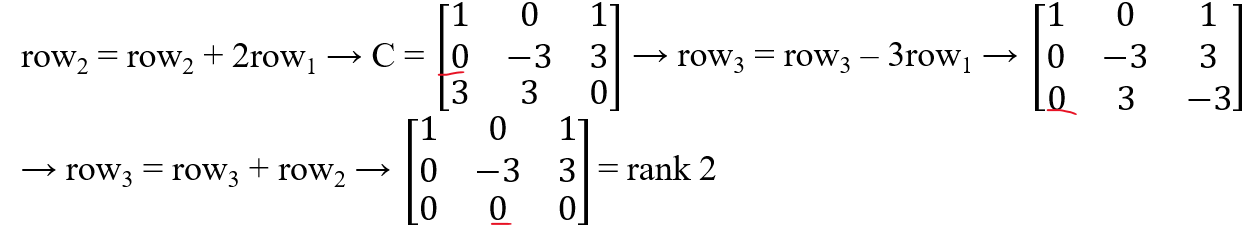
이 경우 3행이 다른 애들과 선형 독립이 아니었던 것.
따라서 행렬 C의 rank는 2.
■ Singular Value Decomposition 특이값 분해
A = UΣV*
< 방법 >
1) AAT를 구하고, 대각 성분에 -λ을 한 후 derterminant(AAT) = 0을 푼다. => λ 나옴
2) AAT에 λ를 넣고, { x1, x2 } 랑 곱해서 0이 나오도록 하는 x1, x2를 찾는다. 그리고 정규화해서 U에 넣는다.
3) ATA에도 같은 λ를 이용해 x1, x2를 찾아서 정규화해서 V에 넣고, V*를 해준다.(실수 범위에서 V* = VT)
m×n 행렬 A의 SVD(Singular Value Decomposition)는 다음과 같은 공식으로 표현됩니다: A = UΣV*
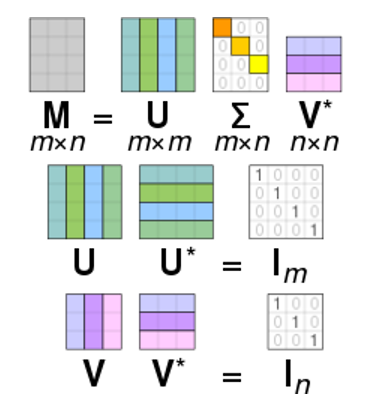
여기서:
U: m×m 크기의 복소수 단위행렬(complex unitary matrix). AAT
Σ: m×n 크기의 직사각형 대각행렬(rectangular diagonal matrix)로, 대각선에는 σi가 존재합니다.
다시말해, ATA의 eigen value의 루트값, 즉 A의 특이값(singular values)이 위치함! 보통 내림차순으로 정렬.
V: n×n 크기의 복소수 단위행렬(complex unitary matrix). ATA
V위에 붙은 첨자 *는 conjugate transpose (켤레 전치)를 의미합니다.
※ 단위행렬(unitary matrix)이란?
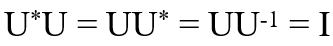
를 만족하는 U를 단위행렬이라고 한다.
실수 범위에서 다루는 경우, 허수부가 사라져서 conjugate transpose(켤레 전치) 대신 transpose(전치)로 다룰 수 있음:
A = UΣV^T
0이 아닌 특이값의 개수는 A의 랭크(Rank)와 같습니다.
U의 열과 V의 열은 각각 A의 좌 특이벡터(left-singular vectors)와 우 특이벡터(right-singular vectors)라고 불립니다.
이들은 각각 u1, ..., um과 v1, ..., vn이라는 직교 정규화(orthonormal)된 기저(bases)로 구성됩니다.
■ Geometric meaning of SVD
SVD의 기하학적 의미에 대해 알아보자.
우선 Eigen Vector 및 Eigen Value의 기하학적 의미이다.
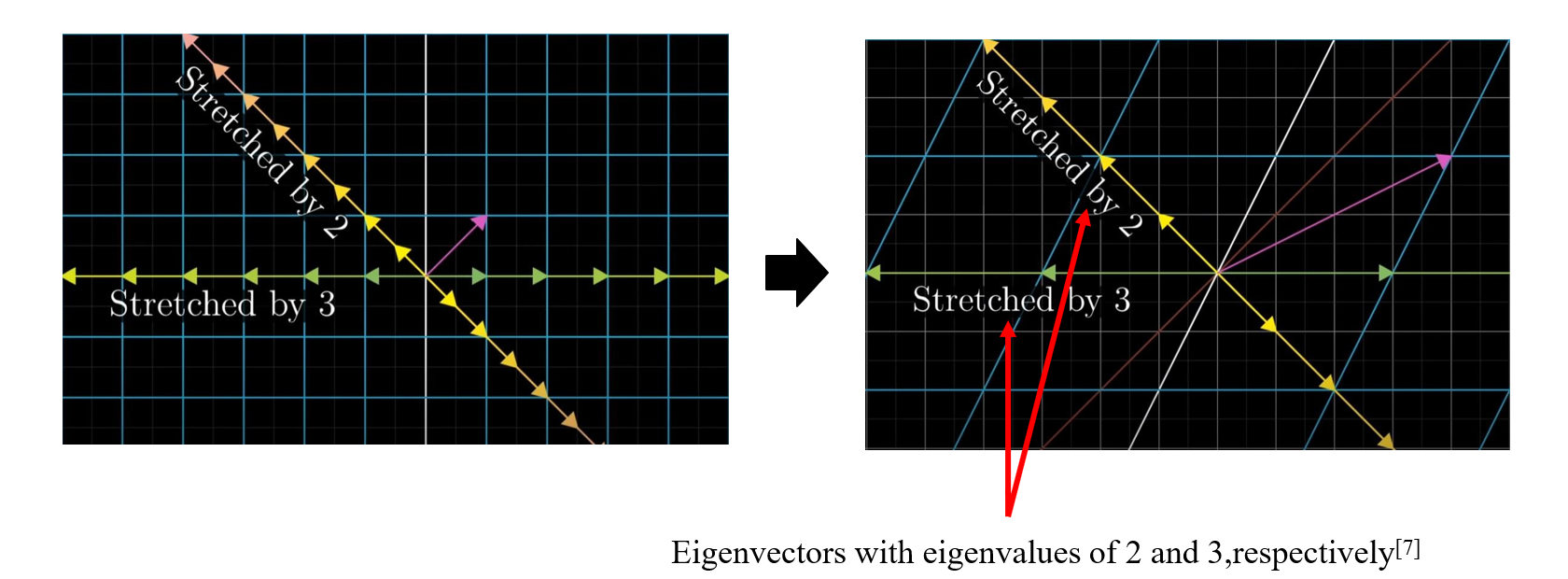
고유벡터는 변환(transformation)에 의해 늘어나는 방향을 가리키는 벡터입니다. "어떤 방향으로 늘릴 거냐"
고유값은 그 늘어나는 정도를 나타냅니다 (만약 고유값이 음수이면, 방향이 반대로 됩니다). "얼마나 늘릴거냐"
그러면 SVD는 기하학적으로 뭘 말하는거냐!
A라는 선형 변환 행렬(선형이므로, translation이 아닌, rotation이나 scaling 이겟죠)을 UΣV*로 분해해서 표현을 해보자.
직관적으로 이해하기 쉽게!
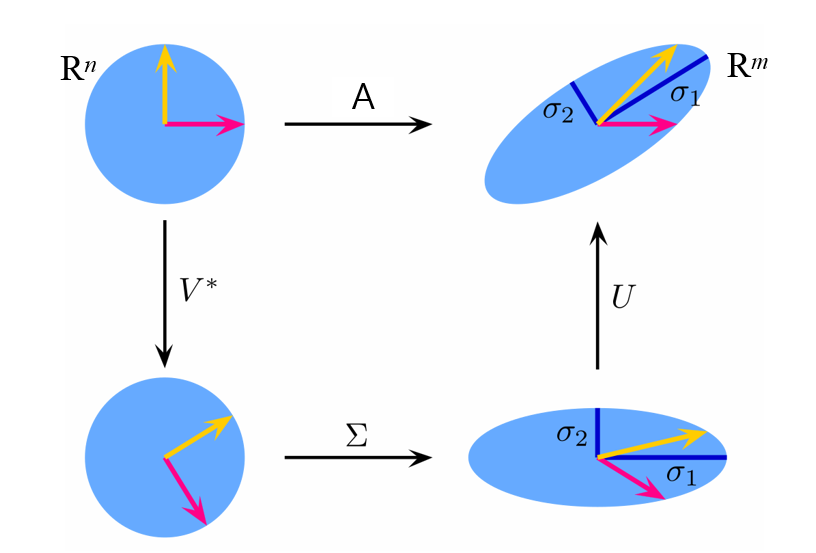
Transformation A가 너무 복잡한거야. 돌리고 늘리고 회전하고 하는데, 뭘 한건지 잘 모르겟어..
[SVD 장점]
■ SVD 계산
앞서 말했듯, 실수 범위에서 SVD는 다음과 같이 계산할 수 있다.
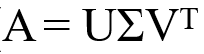
ATA의 고유벡터는 V의 열을 구성합니다.
AAT의 고유벡터는 U의 열을 구성합니다.
Σ의 주대각선은 AAT와 ATA에서 얻은 특이값(고유값의 제곱근)으로 구성되어 있습니다.(AAT와 ATA는 고유값이 똑같이 나옴!)
※ SVD 예제

U구하고 V 구할 때, 공식 안쓰고 ATA 에다 람다값 빼서 계산해도 됨.
단, 순서 잘 맞도록 해야함. 항상 x1=t로 두고, t로 묶어서 빼주는 방식.
t 하나로 안될때(0 나올 때)는, s, r.. 다양한 애들로 x2, x3.. 를 설정해주고, 이로부터 t와의 관계성을 구해서 치환 ㄱㄱ
◆ Pseudo Inverse
우리는 앞서, IK 문제를 푸는것을 다음 수식을 푸는 것으로 정의했다.(https://grace7040.tistory.com/67)
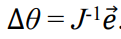
end effector들의 위치가, end effector들의 target 위치로 움직이도록 하는 JΔθ를 의미.
간단히 요약하자면, 아주 짧은 시간 t동안 이동한 호의 길이는 Jacobian이 Δθ만큼 움직인 JΔθ와 같다는 수식.
근데 J inverse은 구하기 어려우니까, J pseudo inverse (J+)를 구해서 접근하기로 했었음.
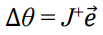
이걸 어떻게 구하는지 알아볼 것임.
Pseudo Inverse 구하는 방법으로, 두가지가 있음.
- moore-penrose 방법
- SVD 방법
◆ Moore-Penrose Pseudo inverse
A+=(ATA)-1AT
행렬 A에 대한 Pseudo inverse A+는 별도의 표기가 없으면 Moore-Penrose inverse임. (일반적으로 동의어로 사용됨)
이는 해가 없는 선형 방정식의 best fit (least squares) 해를 찾는 데 사용됨. (오차가 가장 적은 해)
위 식을 유도하기 위해서 다음 과정을 보자.
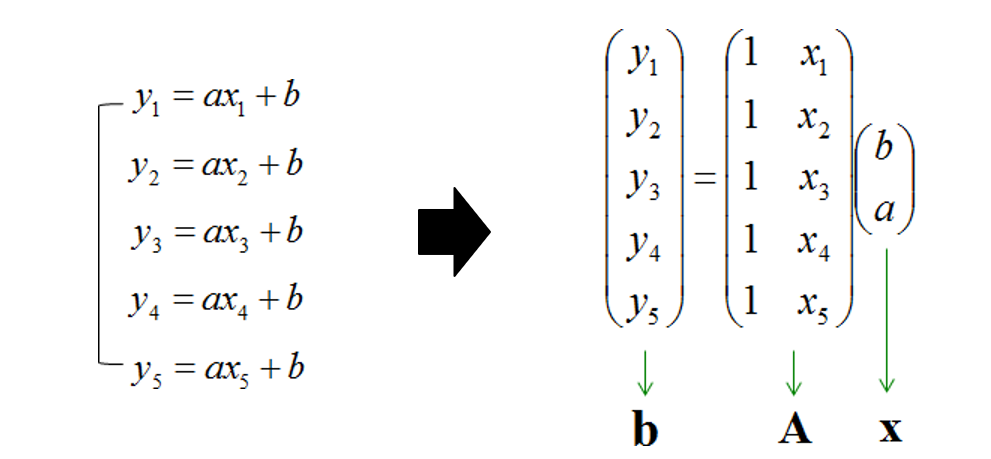
Least Sqaure Method란,
그림처럼 방정식의 개수가 미지수의 개수보다 많은 (overdetermined) 경우의 연립 방정식를 풀기 위한 방법을 의미한다.
이러한 문제에서 방정식의 개수가 미지수의 개수보다 많아지는 이유는 오차를 최소화하기 위해 반복적인 측정이 이루어지기 때문임. 이때문에 overdetermined된, 그리고 종종 일관성이 없는(inconsistent) 선형 방정식들이 생성됨.
overdetermined된 애들은 각자 자기 주장만 하지, 해를 구하는 데 도움은 안 됨.
평면 위에 있는 한 점의 운동을 관찰한다고 가정해보자. 관찰 결과, 이 점이 y = dx + c를 따라 움직인다고 의심된다고 하자.
(x1, y1), (x2, y2), (x3, y3)에서 관찰한 결과를 다음과 같이 표현할 수 있음.
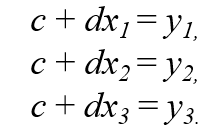
만약 에러(노이즈)가 없다면, 연립 방정식이 그냥 풀릴 것임
그러나 에러가 있다면 연립 방정식이 풀리지 않을 것임. ㅜㅜ
그런 경우에 다음과 같이 일부러 에러를 슬쩍 넣어서 풀어 주는 것을 Least Sqaure Method라고 함.
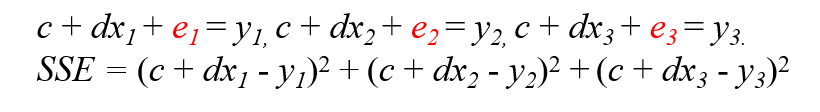
이때 에러를 최소화하는 방향으로 가야함ㅇㅇ
에러를 최소화 하기위한 과정을 살펴보자.
평면 위에서 움직이는 점을 와 같은 형태로 표현할 수 있음.
이때 e는 에러 벡터. 에러도 여러 개 나올 수 있으니까 벡터 형태로 표현함

이때 우리의 목표는 eTe를 최소화하는 것이다! (==에러 제곱들의 합)
다음은 e = y-Ax를 대입해, eTe를 최소화하는 과정이다.
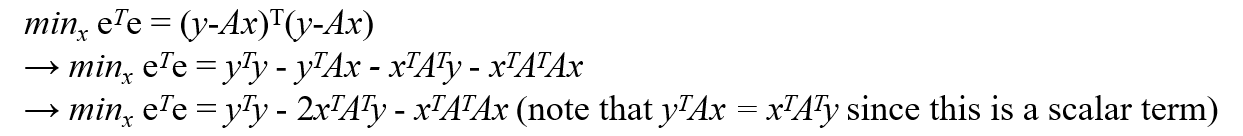
이때, xT로 편미분 했을 때 0이 되는 지점이 eTe의 최솟값임.
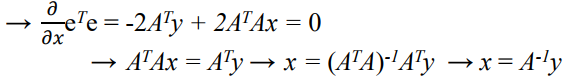
따라서 A+를 다음과 같이 정의할 수 있다!
A+ = 내학점
예제)
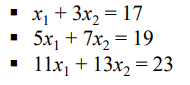
일때, M의 Moore-penrose Pseudoinverse를 구하라.
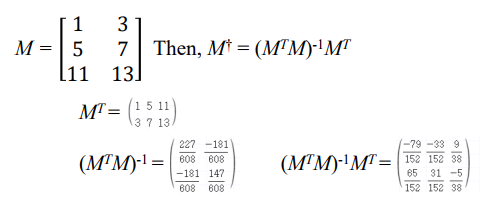
◆ Inverse and SVD
이번에는 SVD를 이용해 pseudo inverse를 계산하는 방법을 알아볼 것.
그전에, SVD를 이용해 그냥 inverse를 계산하는 방법부터 알아볼 것이다.
앞에 썼던 moore-penrose는 특정 조건이 만족할 때만 사용할 수 있었음~
moore-penrose의 경우
행렬 A의 열들이 선형독립인 경우에만 사용가능함. ATA의 inverse가 존재해야 하므로.
(full row rank나 full column rank인 경우에만 가능하다는 뜻!)
먼저 SVD를 사용하여 역행렬을 계산하는 방법을 살펴봅시다.
역행렬이 존재하려면, 정사각 행렬이어야 하므로, 행렬 A가 mxm 행렬이라고 하자.
그럼 U도 mxm, V도 mxm이고 Σ 역시 다음과 같이 mxm일 것임.

앞서 언급했듯, 𝜎i는 행렬 A의 특이값(singular values)으로 정의되며,
U의 열은 좌 특이벡터(left singular vectors)로 불리고, V의 열은 우 특이벡터(right singular vectors)로 불림.
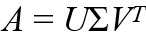
A의 SVD는 위와 같다. 양 변에 inverse를 취해보자. U와 V는 직교하므로, UT = U-1이다. (U-1U = UTU = I)
따라서 A의 역행렬은 다음과 같이 표현할 수 있다.
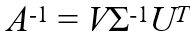
이때 Σ-1는 다음과 같다.
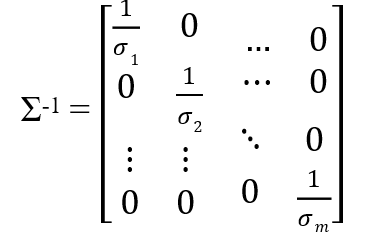
굿! A inverse를 쉽게 구할수 있다.
그런데... 얘도 약간의 제약이 있다. 아래에 설명!
◆ Pseudo Inverse and SVD
A+ = VΣ+UT 해라. (기존 SVD식 양 변에 pseudo inverse 취해준 것)
이때, Σ+에 들어가는 특이값 𝜎중에, 0 아닌 애들만 역수 취해라~ 0은 그대로 두고!
SVD는 역행렬을 구하는 데에 강력한 도구이지만,
목표 행렬 A가 정사각 행렬이 아닌 경우(overdetermined 시스템에서는 A가 유일한 해(역행렬)을 갖지 않기 때문)
또는 A의 어떤 특이값이 0인 경우(1/0은 존재하지 않기 때문)에는 사용할 수 없다는 제약이 있다.
보다 구체적으로 말하자면, 만약 행렬 A의 어떤 특이값 𝜎𝑖 = 0이라면, 어떤 것과 곱해도 0이 되므로 이 정보를 복구할 수 없다.(x*0 = 0일 때 x가 뭔지 알 수 없는 느낌). A𝑥로부터 𝑥를 복원할 수 없다는 뜻.
우리가 할 수 있는 최선은, 0으로의 곱셈에 의해 파괴되지 않은 𝑥의 성분을 복구하는 것입니다.
모든 복구 가능한 정보를 복구하는 행렬을 유사역행렬(pseudo-inverse)이라고 하며, 일반적으로 A+로 표기됩니다. 우리는 SVD를 통해 유사역행렬을 얻을 수 있습니다. 이를 위해서는 Σ에서 0이 아닌 모든 특이값을 역수로 취하고, 0인 특이값은 그대로 0으로 두면 됩니다. 즉, 0보다 큰 특이값에 대해서만 역수를 취하자는 것.
이제 mxn 크기의 행렬로 가져와보자.
mxn 행렬 A에 대해, U는 mxm이고 V는 nxn일 것.
이때 A+를 다음과 같이 쓸 수 있다. (U와 V는 직교행렬이라서, inverse랑 Transpose랑 같음)
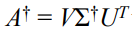
여기서 Σ+는 다음과 같다.

최대한 Singular vector 를 0으로 만들지 않는 방향으로 가자~ 하는 느낌.
0 아닌 애들만 뒤집어라~ 0은 그대로 두고!
◆ Jacobian Pseudo Inverse
이제 IK로 돌아와보자!
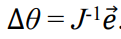
Jacobian 행렬이 정사각 행렬이 아니거나, 역행렬이 존재하지 않을때(비가역; invertible) Jacobian pseudo inverse를 쓴다.
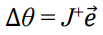
J+는 n × m 행렬로, J의 유사역행렬(pseudo-inverse)이라고 불립니다.
이는 least-squares의 관점에서 방정식 J∆θ = 𝑒에 대한 최적의 해를 제공합니다.
pseudo inverse 방법은 다음과 같이 Moore-Penrose 역행렬을 사용하여 유도될 수 있습니다:
• Jacobian 행렬의 차원에 따라 다음 중 하나의 곱셈을 선택합니다:
- 만약 m ≥ n (tall 또는 square 행렬)이고 J가 full column rank (rank(J) = n)인 경우, JTJ를 계산합니다. (nxn)
(==세로로 길고, 각 행들이 선형독립인 경우) - 만약 m < n (wide 행렬)이고 J가 full row rank (rank(J) = m)인 경우, JJT를 계산합니다. (mxm)
(==가로로 길고, 각 열들이 선형독립인 경우) - 행렬 J가 full row rank나 full column rank가 아닌 경우, SVD를 사용하여 J+를 얻을 수 있습니다.
(각 행, 각 열 모두 선형독립이 아닌 경우)
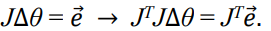
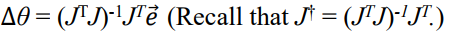
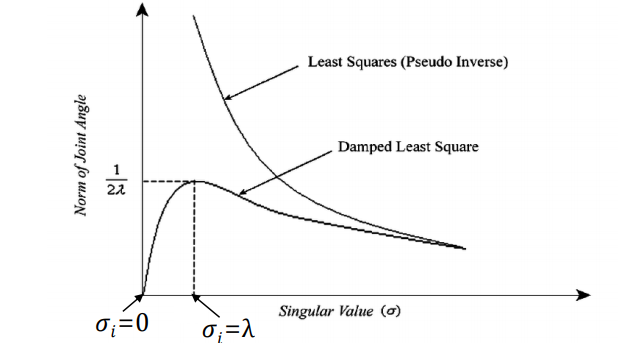
◆ Damped Least Squares (DLS)
J+를 구할 때, Singular value가 0이 되는 것을 막기 위해 약간의 값을 더해줌.
damping value를 설정함으로 인해서 singularity problem을 효과적이고 안정적으로 해결할 수 있다~
Singularity problem, 즉 0인 람다에 죽지 마!
Singular value가 0이 될 때 생기는 문제를 SVD를 이용해 0이 되지 않도록 하는 방법.
DLS는 Singular value가 0이 되는 것을 막기 위해 약간의 값을 더해줌.
- 이 방법에서는, λ를 0이 아닌 damping constant로 둔다.
- damping constant를 잘 골라서 numerically stable하게 만들어야 함.
- damping constant가 너무 작으면 singular value가 0이 되어 발산할 위험이 있으므로 적당히 큰 값을 골라야 함.
- damping constant가 너무 크면 convergence rate가 너무 느려짐. → 알맞은 해를 찾는데 오래 걸린다는 뜻
- DLS에서는 단순히 J∆θ - 𝑒를 최소화하는 ∆θ를 찾는 게 아니라, || J∆θ - 𝑒 ||² + λ²||∆θ||²를 최소화하는 ∆θ를 찾는다.

즉, DLS의 솔루션은 다음과 같다.
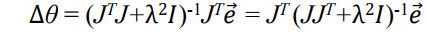
그럼 이제 JJT + λ²I를 구해야 함. 이때 SVD를 사용함.
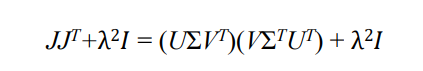

결과적으로 J+는 다음과 같다.
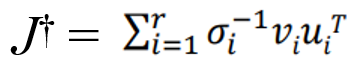
damping value인 λ 근처에서는 그래도 믿을만하게 풀렸따! 라는 뜻
damping value를 설정함으로인해서 singularity problem을 효과적이고 안정적으로 해결할 수 있었다~
'게임 > Inverse Kinematics' 카테고리의 다른 글
| 6. Heuristic Inverse Kinematics Algorithms (0) | 2023.05.30 |
|---|---|
| 5. Quasi-Newton Method for Inverse Kinematics (0) | 2023.05.29 |
| 4. Newton Method for Inverse Kinematics (0) | 2023.05.29 |
| 2. Numerical Solution of Inverse Kinematics (0) | 2023.04.25 |
| 1. Introduction to Inverse Kinematics (0) | 2023.04.08 |




