센로그
6. Heuristic Inverse Kinematics Algorithms 본문
대충 잘~ 그럴듯하게 IK를 푸는 법에 관한 이야기.
뉴턴 방법은 느리고 풀기 어려우나, 정확성을 요구하는 로보틱스 분야에서 많이 사용한다.
FABRIK과 같은 Heuristic Algorithm은 실시간 속도가 중요하고 그럴듯하게 보여야 하는 게임 분야에서 많이 사용한다.
다음의 휴리스틱 IK 알고리즘들을 살펴볼 것임
- CCD
- Triangulation IK
- SIK
- FABRIK
- FABRIK 확장
◆ Cyclic Coordinate Descent (CCD)
Inward: end effector ~> root joint까지 joint 단위로 시행하며, 임계점까지 반복.
각 step마다 end effector가 target position에 최대한 가깝게 하는 방향으로 각 joint를 돌림.
CCD는 휴리스틱 알고리즘의 시초.
관절체의 interactive한 control에 잘 맞는 반복적 heuristic 기술이다. 즉 IK에 좋은 기술이다.
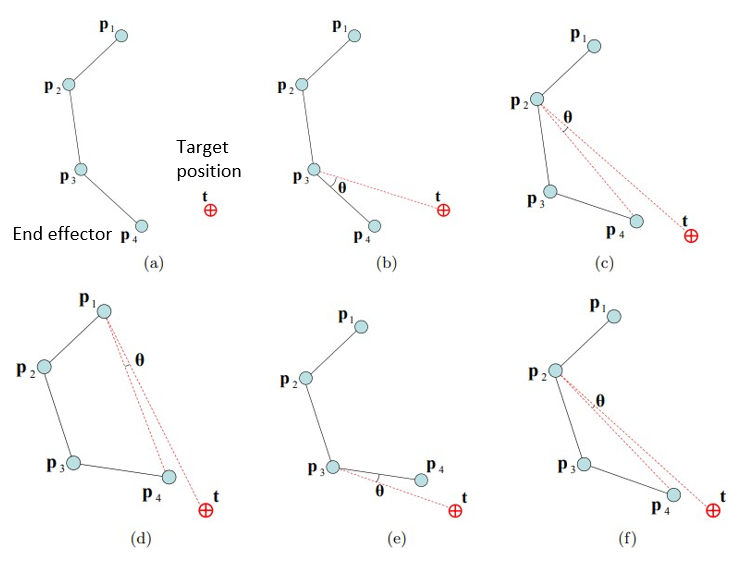
CCD는 한번에 한 개의 joint를 옮김으로써, position과 orientation 에러를 최소화하고자 하는 방법.
< 방법 >
- end effector (p₄)부터 시작해서, root joint (p₁)를 향해서 한 joint씩 나아감. (p₄ - p₃ - p₂ - p₁ - p₄ ...로 Inward하게)
- 이때 각각의 joint는 end effector (p₄)가 최대한 target position (t)과 가까이 있도록하는 방향으로 움직여야 함.
(그림에서 θ가 최대한 0에 가깝게 움직이도록 함) - 이 과정이 우리가 만족할 만한 결과값이 나올 때까지 반복됨.
=> 각각의 joint들에 대한 계산 비용이 낮아서, 굉장히 빠르게 해를 구할 수 있다.
◆ Triangulation IK
outward: root joint ~> end effector 쪽으로 진행.
non-iterative라 빠름. 그러나 비현실적(ㄱ자)
제2 코사인 법칙을 이용해서 푸는 방식.
이번에는 root joint부터 시작해서, kinematic chain을 따라 end effector 쪽으로 나아감. (outward하게)
Unconstrained joint(이 관절은 몇 도 이상 꺾이면 안돼! 같은 제한이 없음)를 사용했고,
target이 내가 닿을 수 있는 거리에 있으면, 항상 답을 찾을 수 있다는 게 보장된다.
< 방법 >
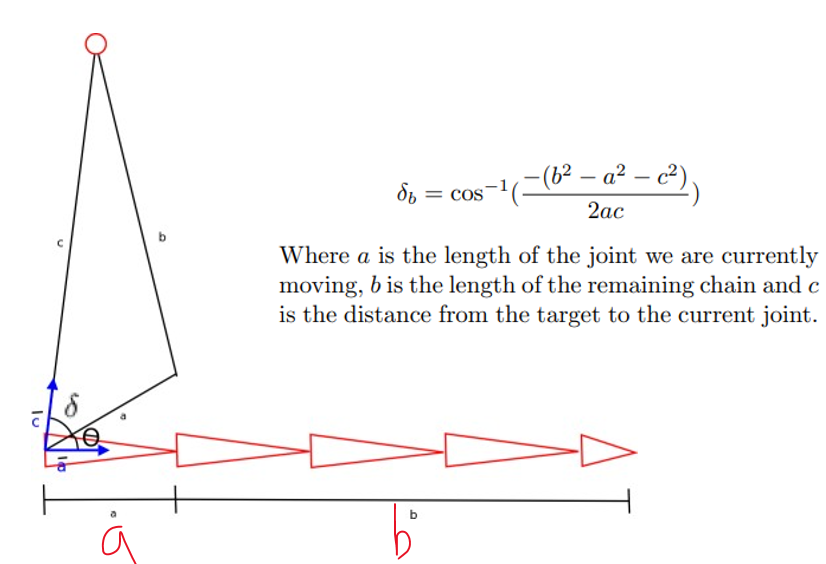
- 우선 root joint로부터 가까운 첫번째 joint를 a로, 나머지를 전부 b로 두고 쫙 편다.
- 그 다음에 a를 한번 굽히고, b를 한번에 굽혀서 직선 쭉~
=> iteration을 돌지 않기 때문에 CCD보다도 더 빠름.
근데 이렇게 풀면, 비현실적이다! 문제점이 많다!

- 당연하게도 end effector 근처에 있는 joint들은 직선으로 연결되어서 그림처럼 비현실적으로 ㄱ자로 꺾임
- 따라서 end effector가 하나인 경우에만 올바르게 작동할 것임. (복잡한 캐릭터 모델에는 사용 못 함)
- 또, constraint가 있으면 답을 풀 수 없다는 단점. constraint가 있는 풀리는 문제일지라도 못 풀 수 있음.
현실의 대부분 joint들은 constraint가 존재하는데 이게 웬말..
◆ Sequential Inverse Kinematics (SIK)
실시간 3D 휴먼 풀 바디 재구성
root joint → spine → clavicles(보는 방향) → 팔다리 순으로 결정
SIK는 실시간으로 3D human full body movement를 재구성하는 IK 방법이다.
input으로 end effector positions(한 개만 넣는 게 아니라, wrist, ankles, head, pelvis 등 여러 개를 넣음)을 넣어주면,
이를 이용해 human pose를 찾는다.
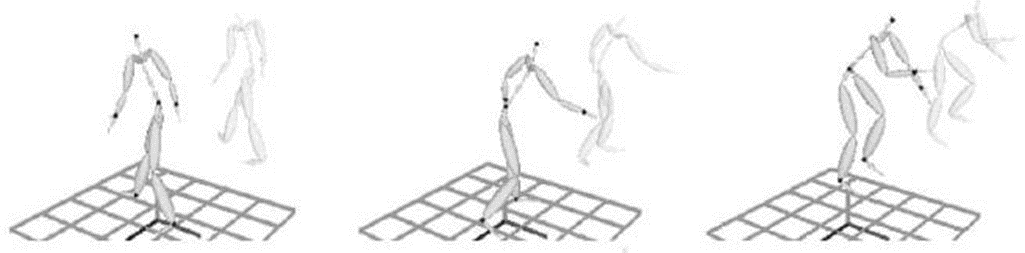
< 과정 >
- root joint를 찾는다.
- root와 head의 위치와 방향으로부터 spine(척추)를 만든다.
- 우리가 찾은 spine 위치와 end effector 위치를 바탕으로, clavicles(쇄골)의 방향을 결정한다.
(어디를 보고있는지 결정한다는 의미) - 이제 end effector 위치를 기준으로 팔, 다리를 만든다.
◆ Forward and Backward Reaching Inverse Kinematics (FABRIK)
앞에서 살펴본 애들은 사실, 필요한 데이터가 많거나 비현실적이거나 constraint 있으면 안 풀리거나..
암튼 그다지 좋은 기술이 아님.
이때 등장한 것이 FABRIK(패브릭)! Unreal이나 Unity 엔진에서도 실제로 FABRIK을 사용한다.
이름 그대로, 앞으로(forward)도 가고 뒤로(backward)도 간다.
root joint ↔ end effector로 가는 방향을 말하는 것임. 앞으로도 iteration 한번 돌고, 뒤로도 iteration 한번 돌고.. 이런 방식
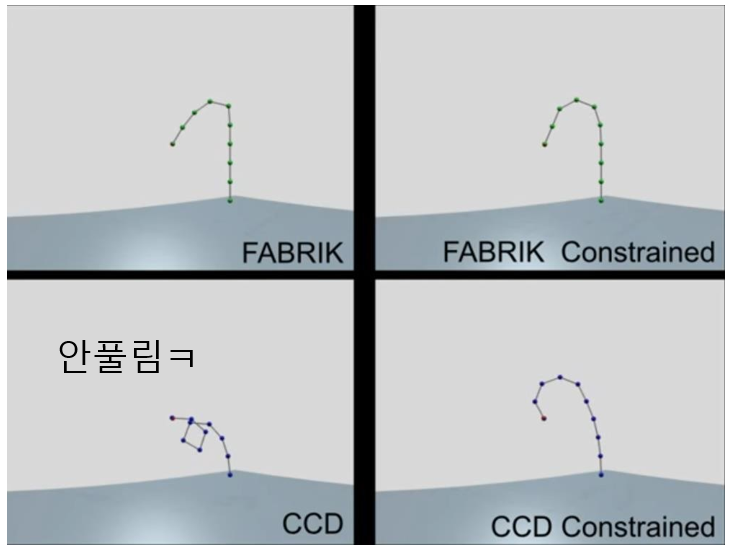
FABRIK은 각 joint angle을 한번씩만 조정해서, error를 최소화하는 방향으로 움직인다.
< 방법 오버뷰 >
- end effector부터 시작해서, backward로 올라가면서 각 joint를 조정한다.
- 그러고 나서 다시 root joint로부터 시작해서, forward로 내려가면서 각 joint를 조정한다.
이때, rotation 관점에서 생각하는 게 아니라, position 관점에서 생각해서 문제를 푼다!
rotation은 quaternion이나 대수기하학 같은 거 쓰기 때문에 연산하기 힘들곤 했음 ㅇㅇ
position은 그냥 심플하게 풀리니까 사용하기 쉽다~
이를 통해 더 적은 iteration으로 수렴하고, 계산 비용도 더 적고, 보다 현실적인 자세를 생성한다.
따라서 heuristic IK algorithm에서는 position을 많이 사용하곤 함!
◆ FABRIK - 구체적 과정
backward : end effector을 target으로 옮기고, 다음 joint들부터는 bone 크기만큼 당겨주면서 올라감
forward : root joint에 도달하면 root를 다시 원 위치로 올려주고, 내려가면서 bone 크기만큼 다시 당겨줌
※ single end effector인 경우 사용 가능
FABRIK을 구체적으로 알아보기 위해 parameter 세팅을 살펴보자.
우선, 우리는 end effector 가 하나인 간단한 구조를 가정하도록 한다.
- p₁~ pn : joint의 position. (이때 p₁은 root joint이고, pn은 end effector를 의미)
- t : target position
- b : 초기 base position
- d : 거리 (그림 참고)
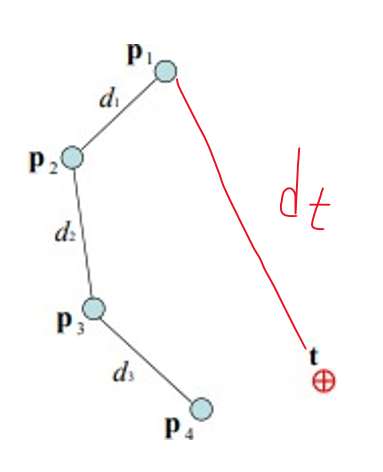
single target이고, 4개의 joint가 있으니 p₁~p₄를 설정한다.
< 과정 >
1. 각각 joint들 사이의 distance를 구한다.
2. target에 닿을 수 있는지 없는지를 판단한다.
root와 target의 거리를 dt라고 할 때, dt < d₁+d₂+d₃ 이면 닿는 것 ㅇㅇ
3. target이 닿을 수 있는 곳에 있다면, forward/backward full iteration을 돈다.
4. 첫 stage(forward)
- 4.a. end effector p₄부터 시작해서 root joint p₁까지 inward로 올라가면서 joint position을 설정한다.
- 4.b. end effector p₄를 target position t로 옮긴다. p₄의 새로운 위치를 p₄` = t라고 해보자.
- 4.c. 그 다음에 p₃와 p₄` 를 잇는 l₃을 구한다.
- 4.d. p₃의 새로운 위치 p₃`는 l₃ 위에 있어야 할 것이다. 이때 p₃`는 p₄`로부터 d₃ 만큼 떨어진 곳에 위치시킨다.
- 4.e. 이 작업을 root joint까지 반복한다.
- 4.f. 최종적으로는, root joint인 p₁ 또한 어느정도 움직여서 p₁`이 될 것이다. 그런데 root는 움직이면 안됨!
따라서 반대방향으로 iteration을 한번 더 돌 것이다.
5. 두번째 stage(backward)
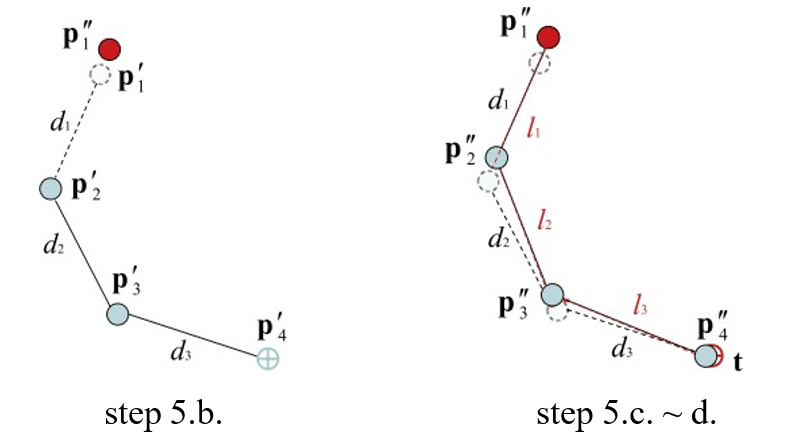
- 5.a. 첫 stage와 같은 작업을 이번에는 root joint로부터 시작해서 end effector까지 outward로 내려가면서 진행한다.
- 5.b. p₁`의 새 위치 p₁`` = 초기 위치로 다시 땡겨준다.
- 5.c. p₁``와 p₂`를 잇는 l₂ 위에, d₁ 만큼 떨어진 거리에 p₂``를 위치시킨다.
- 5.d. 이 작업을 end-effector까지 반복한다.
6. 한번 iteration을 완수하면, end effector이 target과 어느정도 가까워져 있을 것이다.
7. end effector와 target position이 일치하거나, 충분히 가까울 때까지 반복한다.
◆ FABRIK - multi end effectors
앞서 설명한 방법은 single end effector인 경우에만 풀 수 있다.
그러나 IK에 적용할 모델들은 보통 몇 개의 kinematic chain들을 가지고 있고, 각각의 chain들은 1개 이상의 end effector을 가지고 있을 것이다.
따라서 이번에는 multi end effectors인 경우에서도 사용할 수 있도록 확장된 FABRIK 알고리즘을 설명할 것임.
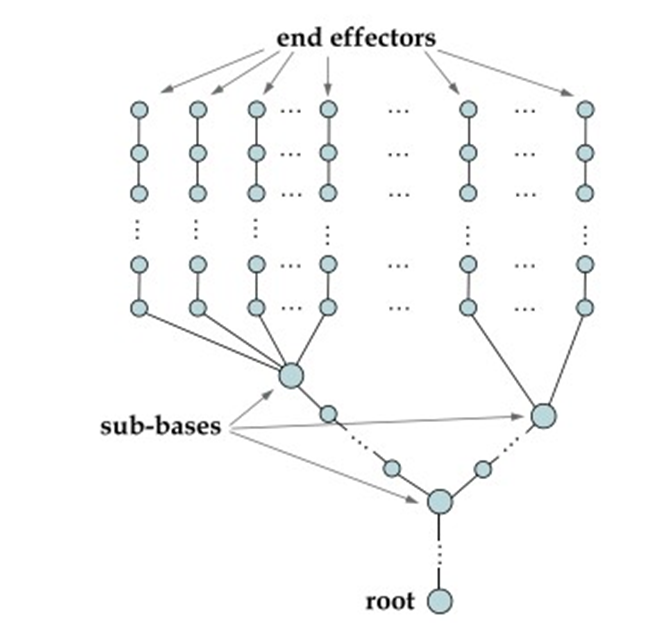
※ sub-base joint : 두개 이상의 chain이 연결되어 있는 joint을 의미함.
예를들어 pelvis에는 왼발 체인, 오른발 체인, 몸 체인, .. 등이 달려있음
< 풀기 위한 조건 >
▷ sub-base joint에 대한 정보와, chian의 구조와 개수를 알고 있어야 함.
물론 게임에서는 기본적으로 모델에 대한 정보를 가지고 있기 때문에 문제가 되지 않음 ㅇㅇ
< 과정 >
첫 스테이지: end-effectors → sub-base, sub-bases → root
- 1.똑같이 end-effector 부터 시작해서 기존 알고리즘(forward)을 수행하는데, sub-base joint까지만(원랜 root까지 갔음) 간다! (end-effector을 target으로 옮기고, 다른애들을 bone 크기만큼 당겨주기)
- 2. 이 과정을 sub-base joint에 연결된 모든 end-effector에 대해 수행하고 나면, 각 end-effector들과 sub-base joint까지를 각각 따로 풀었기 때문에, desired sub-base position이 여러개로 나뉠 것임.
- 3. 휴리스틱 알고리즘 답게 큰 생각 없이, average로 계산해서 sub-base joint의 position을 결정함.
- 4. 이후, sub-base joint로부터 root joint까지 다시 기존 알고리즘(forward)을 수행한다. 다른 sub-base joint가 있다면 이에 대해 또 작업한다.
두번째 스테이지: root → sub-bases, sub-base → end-effectors
- 1. root joint부터 시작해서 기존 알고리즘을 수행(backward)하는데, sub-base joint까지만 간다. (root joint 위치를 원래 있었어야 하는 곳으로 고정시키고, sub-base까지의 다른애들을 bone 크기 만큼 다시 당겨주기)
- 2. sub-base joint에 연결된 각 chain에 대해 독립적으로 작업해서 end-effector까지 진행한다. 다른 sub-base joint가 있다면 이에 대해 또 작업한다.
- 3. end effector와 target position이 일치하거나, 충분히 가까울 때까지 반복한다.
◆ FABRIK - joint limits
매 step마다 가능한 범위 안으로 들어오도록 re-positioning 및 re-orientation 수행.
이때, 3D 문제를 2D상으로 projection해서 풂 => 처리 시간 감소
이번에는, constraint가 주어진 경우를 살펴보자.
대부분의 human body model은 joint들로 이루어져있고, joint들은 현실적인 모션을 위한 rotation 제한을 가지고 있음.
FABRIK은 반복적이기 때문에, 매 step마다 유효한 범위 내에 유지되도록 결과 방향을 조금씩 움직임으로써 joint 제한들은 억지로 적용할 수 있다. 그냥 매 스텝마다 범위 밖에 있다면 가능한 범위 안으로 툭툭 건드려주겠다는 뜻
메인 아이디어는, joint constraint를 만족시키는 곳으로 positioning과 orientation을 다시 해주는 것.
다른 기술들과 비교했을때, 3D에서의 문제를 2D로 가져와서 푼 만큼 복잡도와 처리시간이 줄어듦
θ에 의한 회전 제한(방향별로 깔때기 벌어지는 정도)과 rotor R에 의한 방향 제한이 있는 ball-and-socket joint가 있다고 가정하자. 이런 joint limit 범위는 cone의 형태, 특히 irregular cone의 형태로 정해진다.
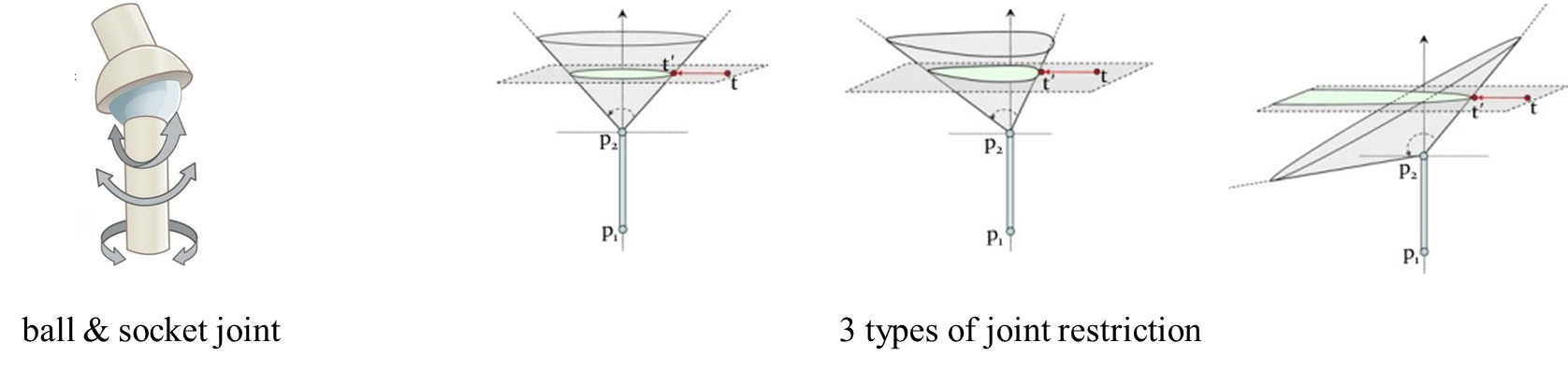
순서대로 하나씩 보자.
- 모든 방향에 대해 θ가 같다면, 가동 범위를 나타내는 conic section은 원을 그리게 될 것.
- 모든 방향에서 θ>90 이거나 θ<90 둘 중 하나인 경우, conic section은 타원(ellipsoidal) 형태가 됨
- θ>90인 θ도 있고, θ<90인 θ도 있는 경우, conic section은 포물선(parabolic) 형태로 잘림.
각 joint마다 이런 limit 범위가 cone 형태로 나타나는 것임.
이중 가장 일반적인 ellipsoidal shape라고 가정하고, 작동 방법을 살펴보자.
4개 방향에서 각각의 rotation constraint를 나타내는 θ₁~θ₄가 정해져있다고 하자.
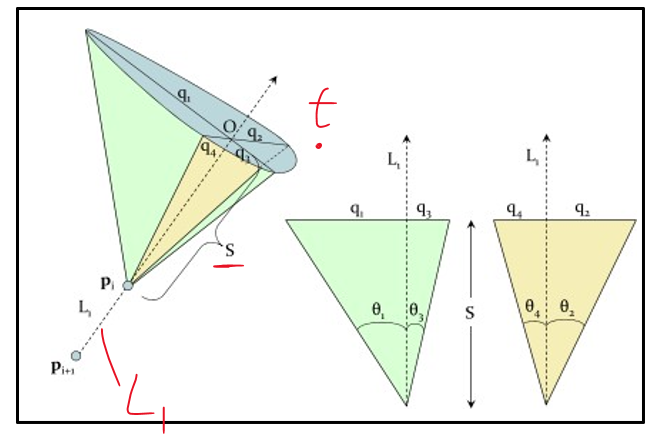
우선 t는 이번에 옮겨야할 joint를 의미한다. 그림에선 pi-1에 해당할 것.
t를 L₁으로 projection 시킨 점을 O라 하자. (당연하게도, O와 t를 한 평면에 있도록 하는 평면이 존재한다.)
O와 joint pi를 이용해 S를 구해준다.
θ₁~θ₄와 S를 가지고 tan 연산을 해주면 q₁~q₄가 나옴. (2D 평면상에서 구동범위 정의)
3D 공간상에서 풀기엔 cost가 크니까, 아래 그림처럼 2D 내에서 풀 수 있도록 projection한 것임.
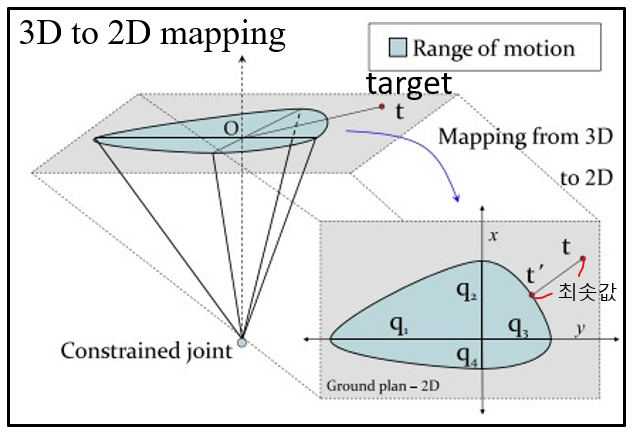
평면에서, t가 현재 구동 범위(타원) 밖에 있기 때문에, 타원 안으로 옮겨줘야 함.
타원 위에 있는 점 중에서, t와의 거리를 최소로 하는 점을 t`이라고 하자. t를 t`으로 옮겨준다.
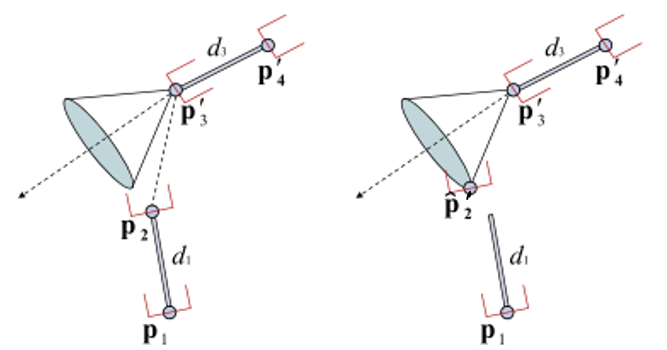
그러고 나서 bone 크기만큼 당겨주고, pi와 t`를 잇는 방향으로 (t`를) 돌린다.
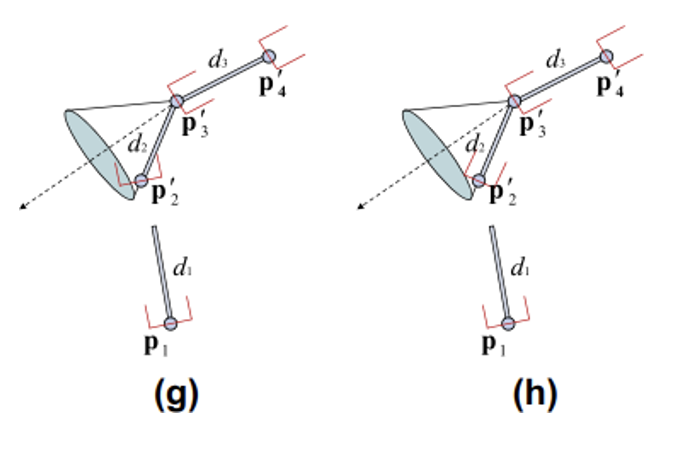
이 다음의 L은 p₃`와 p₂`를 잇는 방향으로 이어질 것임. 이런식으로 쭉 반복~
◆ FABRIK 장점~
그럼 FABRIK이 얼마나 빠르냐~?
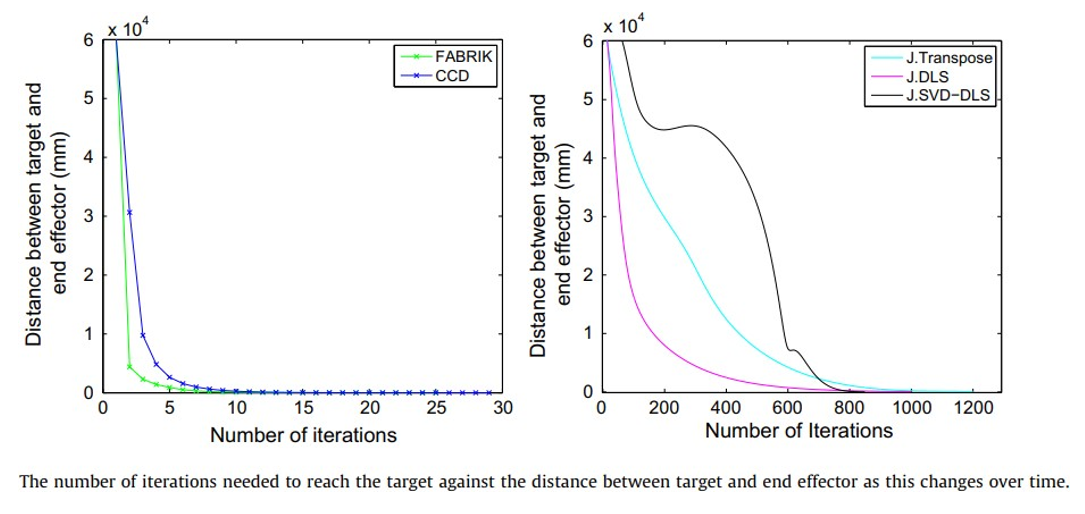
- CCD보다 10배 빠름.
- 자코비안 보다 1000배 빠름.
FABRIK의 강점은, 문제를 그럴듯하게 푼다는 것.
iteration 별로 안 돌아도 타겟을 잘 찾고, 수렴도 잘 하고, 못 닿더라도 최대한 가까이 감!
'게임 > Inverse Kinematics' 카테고리의 다른 글
| 7. Motion Capture and Character Animation (0) | 2023.06.01 |
|---|---|
| 5. Quasi-Newton Method for Inverse Kinematics (0) | 2023.05.29 |
| 4. Newton Method for Inverse Kinematics (0) | 2023.05.29 |
| 3. Jacobian Inverse Methods for Inverse Kinematics (0) | 2023.05.27 |
| 2. Numerical Solution of Inverse Kinematics (0) | 2023.04.25 |




